Branch and Bound

optimizationalgorithmscetztikz

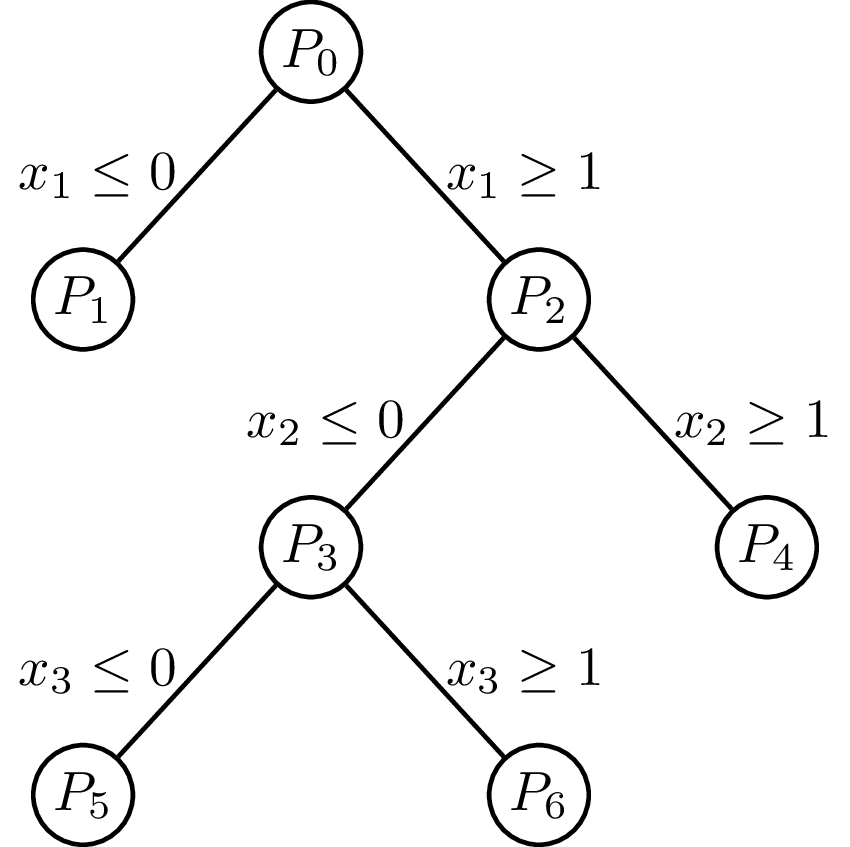
Illustration of a linear-programming (LP)-based branch and bound algorithm. Not knowing how to solve a mixed-integer programming (MIP) problem directly, it first removes all integrality constraints. This results in a solvable LP called the linear-programming relaxation of the original MIP. The algorithm then picks some variable x restricted to be integer, but whose value in the LP relaxation is fractional. Suppose its value in the LP relaxation is x = 0.7. It then excludes this value by imposing the restrictions x ≤ 0 and x ≥ 1, thereby creating two new MIPs. By applying this recursively step and exploring each resulting bifurcation, the globally optimal solution satisfying all constraints can be found.