Harmonic Oscillator Energy vs Angular Frequency
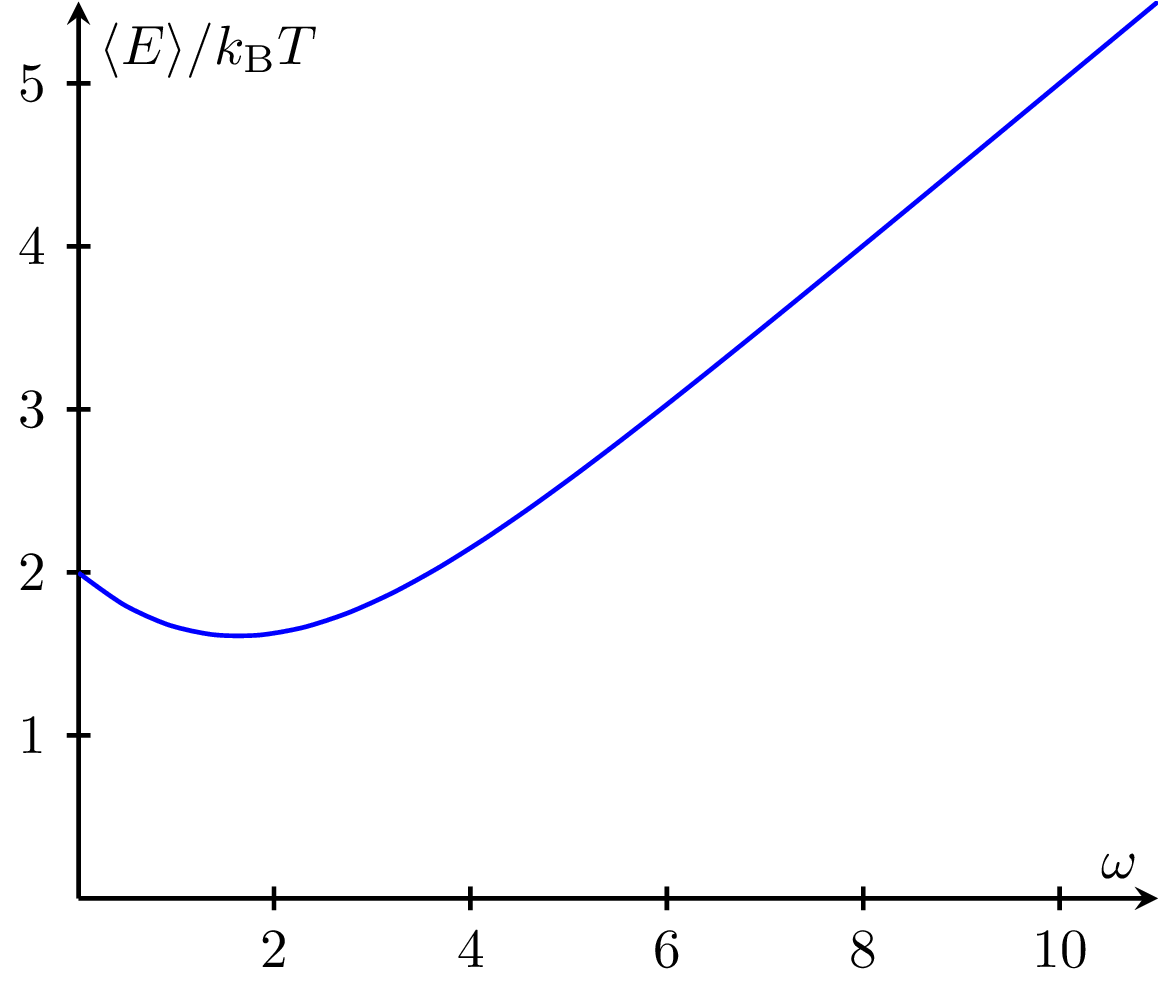
Harmonic oscillator energy $\langle E\rangle/k_\text{B} T$ vs angular frequency $\omega = \sqrt{k/m}$
Download
Code
harmonic-oscillator-energy-vs-freq.typ (42 lines)
harmonic-oscillator-energy-vs-freq.tex (25 lines)