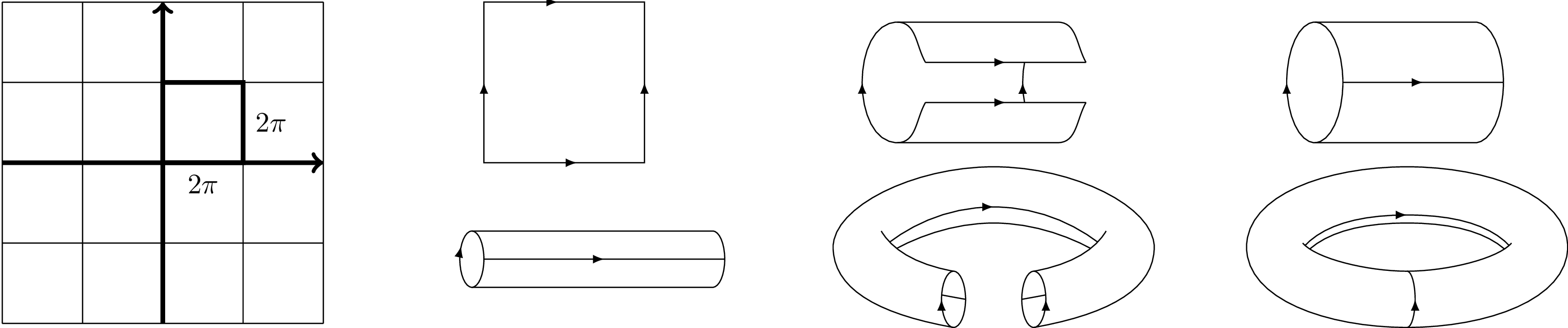
Plane to Torus
Visualization of how a rectangular region of the plane becomes a torus through periodic boundary conditions. The diagram shows the identification of opposite edges and the resulting fundamental domain, a key concept in string theory compactification where spatial dimensions are "curled up" into compact geometries. This construction helps understand modular transformations and the origin of winding modes in string theory.
Download
Code
LaTeX
plane-to-torus.tex (145 lines)
\documentclass[tikz]{standalone}
\usetikzlibrary{decorations.markings,arrows}
\begin{document}
\begin{tikzpicture}
% lattice
\draw[->,ultra thick] (-2,0) -- (2,0);
\draw[->,ultra thick] (0,-2) -- (0,2);
\draw (-2,-2) grid (2,2);
\node [draw,ultra thick,rectangle,minimum width=1cm,minimum height=1cm,label=below:$2 \pi$,label=right:$2 \pi$] at (0.5,0.5) {};
% square
\begin{scope}[xshift=4cm,yshift=1cm]
\draw[postaction={decorate},decoration={
markings,
mark=at position .145 with {\arrow{latex}},
mark=at position .375 with {\arrow{latex}},
mark=at position .635 with {\arrowreversed{latex}},
mark=at position .875 with {\arrowreversed{latex}},
}
]
(0,-1) -- +(2,0) -- +(2,2) -- +(0,2) -- cycle;
\end{scope}
% bracelet
\begin{scope}[xshift=9.5cm,yshift=1cm]
\draw[postaction={decorate},decoration={
markings,
mark=at position .5 with {\arrow{latex}}
}
]
(0,.25) -- ++(2,0);
\draw[postaction={decorate},decoration={
markings,
mark=at position .5 with {\arrow{latex}}
}
]
(0,-.25) -- ++(2,0);
\draw[postaction={decorate},decoration={
markings,
mark=at position .5 with {\arrow{latex}},
}
] (0,-.25) to[out=-120,in=0] (-.35,-.75) to[out=180,in=180] (-.35,.75) to[out=0,in=120] (0,.25);
\draw (2,.25) to[out=120,in=0] (1.65,.75) -- (-.35,.75) (-.35,-.75) -- (1.65,-.75) to[out=0,in=-120] (2,-.25);
\begin{scope}
\clip (0,.25) rectangle (2,-.25);
\draw[postaction={decorate},decoration={
markings,
mark=at position .5 with {\arrowreversed{latex}},
}
] (1.65,.75) to[out=180,in=180] (1.65,-.75);
\end{scope}
\end{scope}
% cylinder
\begin{scope}[xshift=14.7cm,yshift=1cm]
\draw[postaction={decorate},decoration={
markings,
mark=at position .5 with {\arrow{latex}},
}
] (0,0) -- (2,0);
\draw[postaction={decorate},decoration={
markings,
mark=at position .5 with {\arrow{latex}},
}
] (0,0) arc[start angle=0,delta angle=-360,x radius=.35,y radius=.75];
\draw (2,0) arc[start angle=0,delta angle=-90,x radius=.35,y radius=.75] -- ++(-2,0);
\draw (2,0) arc[start angle=0,delta angle=90,x radius=.35,y radius=.75] -- ++(-2,0);
\end{scope}
% long cylinder
\begin{scope}[xshift=4cm,yshift=-1.2cm]
\draw[postaction={decorate},decoration={
markings,
mark=at position .5 with {\arrow{latex}},
}
] (0,0) -- (3,0);
\draw[postaction={decorate},decoration={
markings,
mark=at position .6 with {\arrow{latex}},
}
] (0,0) arc[start angle=0,delta angle=-360,x radius=.15,y radius=.35];
\draw (3,0) arc[start angle=0,delta angle=-90,x radius=.15,y radius=.35] -- ++(-3,0);
\draw (3,0) arc[start angle=0,delta angle=90,x radius=.15,y radius=.35] -- ++(-3,0);
\end{scope}
% open torus
\begin{scope}[xshift=9cm,yshift=-1.7cm]
\draw[postaction={decorate},decoration={
markings,
mark=at position .5 with {\arrow{latex}},
}
] (1,0) arc[start angle=0,delta angle=-360,x radius=.15,y radius=.35];
\draw (1,0) ++(-.15,-.35) .. controls +(170:1) and +(-90:.5) .. ++(-1.5,1) .. controls +(90:.5) and +(180:1) .. ++(2,1) .. controls +(0:1) and +(90:.5) .. ++(2,-1) .. controls +(-90:.5) and +(10:1) .. ++(-1.5,-1) coordinate (a);
\draw[postaction={decorate},decoration={
markings,
mark=at position .5 with {\arrow{latex}},
}
] (a) ++(-.15,.35) arc[start angle=0,delta angle=-360,x radius=-.15,y radius=.35];
\draw (1,0) ++(-.15,.35) .. controls +(170:.5) and +(-60:.25) .. ++(-.9,.5) coordinate (b);
\draw (a) ++(0,.7) .. controls +(10:.5) and +(240:.25) .. ++(.9,.5) coordinate (c);
\begin{scope}
\clip (1,0) ++(-.15,.35) .. controls +(170:.5) and +(-60:.25) .. ++(-.9,.5) -- ++(0,2) -| (c) .. controls +(240:.25) and +(10:.5) .. ++(-.9,-.5);
\draw (1,0) ++(-.15,-.35) ++(0,-.7) .. controls +(170:1) and +(-90:.5) .. ++(-1.5,.8) .. controls +(90:.5) and +(180:1) .. ++(2,1.2) .. controls +(0:1) and +(90:.5) .. ++(2,-1.2) .. controls +(-90:.5) and +(10:1) .. ++(-1.5,-.8);
\draw[postaction={decorate},decoration={
markings,
mark=at position .5 with {\arrow{latex}},
}
] (1,0) ++(-.15,-.35) ++(0,-.8) .. controls +(170:1) and +(-90:.5) .. ++(-1.5,.8) .. controls +(90:.5) and +(180:1.2) .. ++(2,1.5) .. controls +(0:1.2) and +(90:.5) .. ++(2,-1.5) .. controls +(-90:.5) and +(10:1) .. ++(-1.5,-.8);
\end{scope}
\begin{scope}
\clip (a) ++(-.15,.35) arc[start angle=0,delta angle=-360,x radius=-.15,y radius=.35];
\draw (a) ++(-.15,.35) .. controls +(10:1) and +(-90:.5) .. ++(1.5,.8);
\end{scope}
\begin{scope}
\clip (1,0) arc[start angle=0,delta angle=-360,x radius=.15,y radius=.35];
\draw (1,0) .. controls +(170:1) and +(-90:.5) .. ++(-1.5,.8);
\end{scope}
\end{scope}
% torus
\begin{scope}[xshift=14cm,yshift=-1.7cm]
\draw[postaction={decorate},decoration={
markings,
mark=at position .5 with {\arrowreversed{latex}},
}
] (1.5,.35) arc[start angle=90,end angle=-90,y radius=.35,x radius=.1];
\draw (1.5,-.35) .. controls +(180:1) and +(-90:.65) .. ++(-2,1) .. controls +(90:.65) and +(180:1) .. ++(2,1) .. controls +(0:1) and +(90:.65) .. ++(2,-1) .. controls +(-90:.65) and +(0:1) .. ++(-2,-1); \draw (1.5,.35) .. controls +(180:.5) and +(-50:.25) .. ++(-1.3,.35) coordinate (b);
\draw (1.5,.35) .. controls +(0:.5) and +(230:.25) .. ++(1.3,.35) coordinate (c);
\begin{scope}
\clip (1.5,.35) .. controls +(180:.5) and +(-50:.25) .. ++(-1.3,.35) -- ++(0,2) -| (c) .. controls +(230:.25) and +(0:.5) .. ++(-1.3,-.35);
\draw (1.5,-.35) ++(0,-.7) .. controls +(180:1) and +(-90:.65) .. ++(-1.5,1) .. controls +(90:.65) and +(180:1) .. ++(1.5,1) .. controls +(0:1) and +(90:.65) .. ++(1.5,-1) .. controls +(-90:.65) and +(0:1) .. ++(-1.5,-1);
\draw[postaction={decorate},decoration={
markings,
mark=at position .5 with {\arrow{latex}},
}
] (1.5,-.35) ++(0,-.6) .. controls +(180:1) and +(-90:.65) .. ++(-1.5,1) .. controls +(90:.65) and +(180:1) .. ++(1.5,1) .. controls +(0:1) and +(90:.65) .. ++(1.5,-1) .. controls +(-90:.65) and +(0:1) .. ++(-1.5,-1);
\end{scope}
\end{scope}
\end{tikzpicture}
\end{document}