QFT Propagator Poles
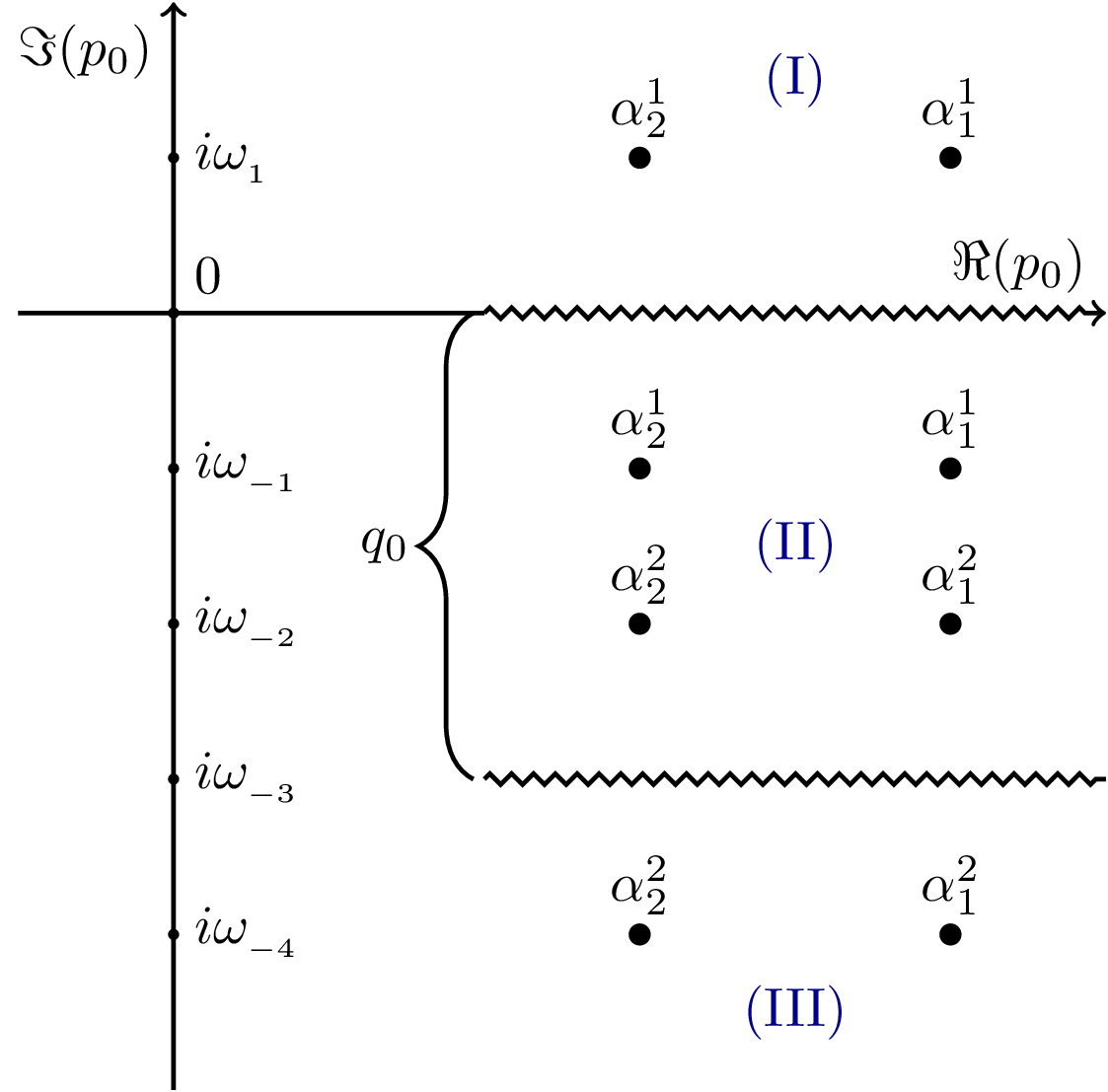
Complex plane visualization of propagator poles and branch cuts in quantum field theory. The diagram shows the analytic structure of Green's functions, including the relationship between retarded/advanced propagators and the placement of poles relative to the real axis. This structure helps understand causality and the connection to Matsubara frequencies.
Download
Code
LaTeX
qft-propagator-poles.tex (41 lines)
\documentclass[svgnames,tikz]{standalone}
\usetikzlibrary{decorations.pathmorphing,decorations.pathreplacing}
\begin{document}
\begin{tikzpicture}[thick]
\def\xrange{6} \def\yrange{4}
% Axes
\draw (-1,0) -- (2,0);
\draw[->,decorate,decoration={zigzag,segment length=4,amplitude=1,post=lineto,post length=3}]
(2,0) -- (\xrange,0) node[above left] {$\Re(p_0)$};
\draw[decorate,decoration={zigzag,segment length=4,amplitude=1}] (2,-3) -- (\xrange,-3);
\draw [->] (0,-\yrange-1) -- (0,2) node [below left=0.2] {$\Im(p_0)$};
\draw[decorate,decoration={brace,amplitude=10pt,mirror},xshift=-2pt] (2,0) -- (2,-3) node [midway,left=8pt] {$q_0$};
% Matsubara frequencies
\foreach \n in {-\yrange,...,-1,1}{%
\fill (0,\n) circle (1pt) node [right] {$i \omega_{_{\n}}$};}
\fill (0,0) circle (1pt) node [above right] {0};
% Poles
\fill
(3,1) circle (2pt) node[above] {$\alpha_2^1$}
(5,1) circle (2pt) node[above] {$\alpha_1^1$}
(3,-1) circle (2pt) node[above] {$\alpha_2^1$}
(5,-1) circle (2pt) node[above] {$\alpha_1^1$}
(3,-2) circle (2pt) node[above] {$\alpha_2^2$}
(5,-2) circle (2pt) node[above] {$\alpha_1^2$}
(3,-4) circle (2pt) node[above] {$\alpha_2^2$}
(5,-4) circle (2pt) node[above] {$\alpha_1^2$};
% Regions
\node[DarkBlue] at (4,1.5) {(I)};
\node[DarkBlue] at (4,-1.5) {(II)};
\node[DarkBlue] at (4,-4.5) {(III)};
\end{tikzpicture}
\end{document}
Typst
qft-propagator-poles.typ (81 lines)
#import "@preview/cetz:0.3.4": canvas, draw, decorations
#import draw: line, content, circle
#set page(width: auto, height: auto, margin: 8pt)
#canvas({
let xrange = 6
let yrange = 4
// Axes styles
let arrow-style = (mark: (end: "stealth", fill: black))
let line-style = (stroke: 0.75pt)
let zigzag-style = (amplitude: 0.1, segment-length: 0.2)
// Main axes
line((-1, 0), (2, 0), ..line-style, name: "x-axis-left")
decorations.zigzag(
line((2, 0), (xrange, 0)),
..zigzag-style,
..line-style,
name: "x-axis-right",
)
content((rel: (-0.3, 0.3), to: "x-axis-right.end"), $"Re"(p_0)$, name: "x-label")
decorations.zigzag(
line((2, -3), (xrange, -3), name: "lower-zigzag"),
..zigzag-style,
..line-style,
)
line((0, -yrange - 1), (0, 2), ..arrow-style, ..line-style, name: "y-axis")
content((rel: (0.8, -0.2), to: "y-axis.end"), $"Im"(p_0)$, name: "y-label")
// Brace for q_0
content(
(2, -1.5),
[#math.underbrace(box(width: 7.5em))],
name: "q0-brace",
angle: -90deg,
)
content((rel: (-0.5, 0), to: "q0-brace"), $q_0$, name: "q0-label")
// Matsubara frequencies
for n in range(-yrange, 2) {
if n != 0 {
circle((0, n), radius: 0.04, fill: black, name: "matsubara-" + str(n))
content("matsubara-" + str(n), $i omega_#n$, anchor: "west", padding: 0.2)
}
}
circle((0, 0), radius: 0.03, fill: black, name: "origin")
content((0.2, 0.1), $0$, name: "origin-label")
// Poles
let pole(x, y, label) = {
circle((x, y), radius: 0.06, fill: black, name: "pole-" + str(x) + "-" + str(y))
content("pole-" + str(x) + "-" + str(y), label, anchor: "south", padding: 0.1)
}
// First row of poles
pole(3, 1, $alpha_2^1$)
pole(5, 1, $alpha_1^1$)
// Second row
pole(3, -1, $alpha_2^1$)
pole(5, -1, $alpha_1^1$)
// Third row
pole(3, -2, $alpha_2^2$)
pole(5, -2, $alpha_1^2$)
// Fourth row
pole(3, -4, $alpha_2^2$)
pole(5, -4, $alpha_1^2$)
// Region labels
let blue = rgb("#00008B") // DarkBlue equivalent
content((4, 1.5), text(fill: blue)[(I)], name: "region-1")
content((4, -1.5), text(fill: blue)[(II)], name: "region-2")
content((4, -4.5), text(fill: blue)[(III)], name: "region-3")
})