Self Attention
Creator: Petar Veličković (original)
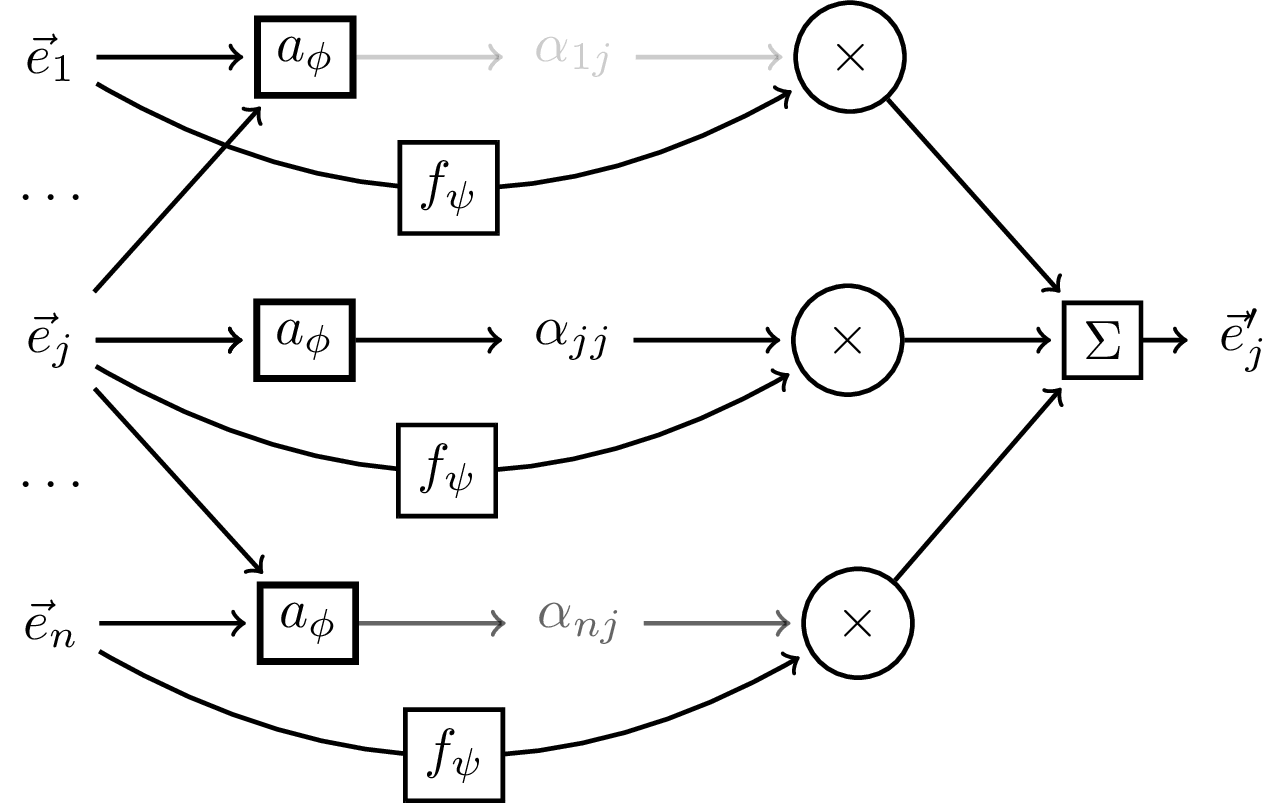
Illustrating the attention mechanism from arxiv:1706.03762.
Download
Code
LaTeX
self-attention.tex (52 lines)
\documentclass[tikz]{standalone}
\usetikzlibrary{positioning}
\begin{document}
\begin{tikzpicture}[shorten >=2pt, thick, ->]
\node (X1) {$\vec e_1$};
\node[rectangle, below=3ex of X1] (x_dots_1) {$\dots$};
\node[below=3ex of x_dots_1] (Xj) {$\vec e_j$};
\node[rectangle, below=3ex of Xj] (x_dots_2) {$\dots$};
\node[below=3ex of x_dots_2] (Xn) {$\vec e_n$};
\node[rectangle, draw, very thick, right=of X1] (attn_1) {$a_\phi$};
\node[rectangle, draw, very thick, right=of Xj] (attn_j) {$a_\phi$};
\node[rectangle, draw, very thick, right=of Xn] (attn_n) {$a_\phi$};
\draw (X1) edge (attn_1) (Xj) edge (attn_1);
\draw (Xj) edge (attn_j) ([xshift=3em]Xj) edge (attn_j);
\draw (Xj) edge (attn_n) (Xn) edge (attn_n);
\node[right=of attn_1, opacity=0.2] (alpha_1j) {$\alpha_{1j}$};
\node[right=of attn_j, opacity=1] (alpha_jj) {$\alpha_{jj}$};
\node[right=of attn_n, opacity=0.6] (alpha_nj) {$\alpha_{nj}$};
\node[circle, draw, right=of alpha_1j] (times_1) {$\times$};
\node[circle, draw, right=of alpha_jj] (times_j) {$\times$};
\node[circle, draw, right=of alpha_nj] (times_n) {$\times$};
\node[rectangle, draw, right=of times_j] (sum) {$\Sigma$};
\node[right=1em of sum] (x_tprim) {$\vec e_j'$};
\draw[opacity=0.2] (attn_1) -- (alpha_1j);
\draw[opacity=1] (attn_j) -- (alpha_jj);
\draw[opacity=0.6] (attn_n) -- (alpha_nj);
\draw (X1) edge[bend right] node[rectangle, draw, fill=white, midway] {$f_\psi$} (times_1);
\draw (Xj) edge[bend right] node[rectangle, draw, fill=white, midway] {$f_\psi$} (times_j);
\draw (Xn) edge[bend right] node[rectangle, draw, fill=white, midway] {$f_\psi$} (times_n);
\draw (times_1) edge (sum) (times_j) edge (sum) (times_n) edge (sum);
\draw[opacity=0.2] (alpha_1j) -- (times_1);
\draw[opacity=1] (alpha_jj) -- (times_j);
\draw[opacity=0.6] (alpha_nj) -- (times_n);
\draw (sum) -- (x_tprim);
\end{tikzpicture}
\end{document}
Typst
self-attention.typ (112 lines)
#import "@preview/cetz:0.3.2": canvas, draw
#import draw: line, content, circle, rect, bezier, set-style
#set page(width: auto, height: auto, margin: 8pt)
#canvas({
set-style(
content: (frame: "rect", stroke: none),
mark: (offset: 0.05),
)
// Define spacing constants
let node-spacing = 2
let layer-spacing = 2
let vertical-spacing = 1.3
// Input nodes
let y1 = 6
let y_dots_1 = y1 - vertical-spacing
let yj = y_dots_1 - vertical-spacing
let y_dots_2 = yj - vertical-spacing
let yn = y_dots_2 - vertical-spacing
let arrow_style = (end: "stealth", fill: black, scale: 0.7)
// First column (input vectors)
content((0, y1), $arrow(e)_1$, name: "arrow1", padding: 2pt)
content((0, y_dots_1), $dots$)
content((0, yj), $arrow(e)_j$, name: "arrowj", padding: 2pt)
content((0, y_dots_2), $dots$)
content((0, yn), $arrow(e)_n$, name: "arrown", padding: 2pt)
// Second column (attention nodes)
let x2 = layer-spacing
content((x2, y1), $a_phi$, frame: "rect", stroke: 1pt, padding: (3pt, 4pt), name: "attn1")
content((x2, yj), $a_phi$, frame: "rect", stroke: 1pt, padding: (3pt, 4pt), name: "attnj")
content((x2, yn), $a_phi$, frame: "rect", stroke: 1pt, padding: (3pt, 4pt), name: "attnn")
// Third column (alpha values)
let x3 = x2 + layer-spacing
content((x3, y1), text(fill: rgb(0, 0, 0, 20%))[$alpha_(1j)$], name: "alpha1j", padding: 3pt)
content((x3, yj), $alpha_(j j)$, name: "alphajj", padding: 3pt)
content((x3, yn), text(fill: rgb(0, 0, 0, 60%))[$alpha_(n j)$], name: "alphanj", padding: 3pt)
// Fourth column (multiplication nodes)
let x4 = x3 + layer-spacing
content((x4, y1), name: "times1", $times$, frame: "circle", padding: 3pt, stroke: .7pt)
content((x4, yj), name: "timesj", $times$, frame: "circle", padding: 3pt, stroke: .7pt)
content((x4, yn), name: "timesn", $times$, frame: "circle", padding: 3pt, stroke: .7pt)
// Fifth column (sum node)
let x5 = x4 + layer-spacing
content((x5, yj), $Sigma$, frame: "rect", stroke: .7pt, padding: 4pt, name: "sum")
// Output node
let x6 = x5 + 1
content((x6, yj), $arrow(e)'_j$, name: "output", padding: 2pt)
// Draw connections
line("arrow1.east", "attn1", mark: arrow_style)
line("arrowj.east", "attnj", mark: arrow_style)
line("arrown.east", "attnn", mark: arrow_style)
line("arrowj.east", "attn1", mark: arrow_style)
line("arrowj.east", "attnn", mark: arrow_style)
line("attn1.east", "alpha1j", mark: arrow_style)
line("attnj.east", "alphajj", mark: arrow_style)
line("attnn.east", "alphanj", mark: arrow_style)
line("alpha1j.east", "times1", mark: arrow_style)
line("alphajj.east", "timesj", mark: arrow_style)
line("alphanj.east", "timesn", mark: arrow_style)
line("times1", "sum", mark: arrow_style)
line("timesj", "sum", mark: arrow_style)
line("timesn", "sum", mark: arrow_style)
line("sum.east", "output.west", mark: arrow_style)
// Draw f_psi connections with labels
for (idx, (start, end)) in (
("arrow1.east", "times1.south-west"),
("arrowj.east", "timesj.south-west"),
("arrown.east", "timesn.south-west"),
).enumerate(start: 1) {
bezier(
start,
end,
(
(v1, v2) => {
let (x1, y1, ..) = v1
let (x2, y2, ..) = v2
return ((x1 + x2) / 2, (y1 + y2) / 2 - 2)
},
start,
end,
),
mark: arrow_style,
stroke: 1pt,
name: "fpsi" + str(idx),
)
content(
"fpsi" + str(idx) + ".50%",
[$f_psi$],
frame: "rect",
stroke: .7pt,
padding: (3pt, 4pt),
name: "fpsi",
fill: white,
)
}
})