home

Chain Homology

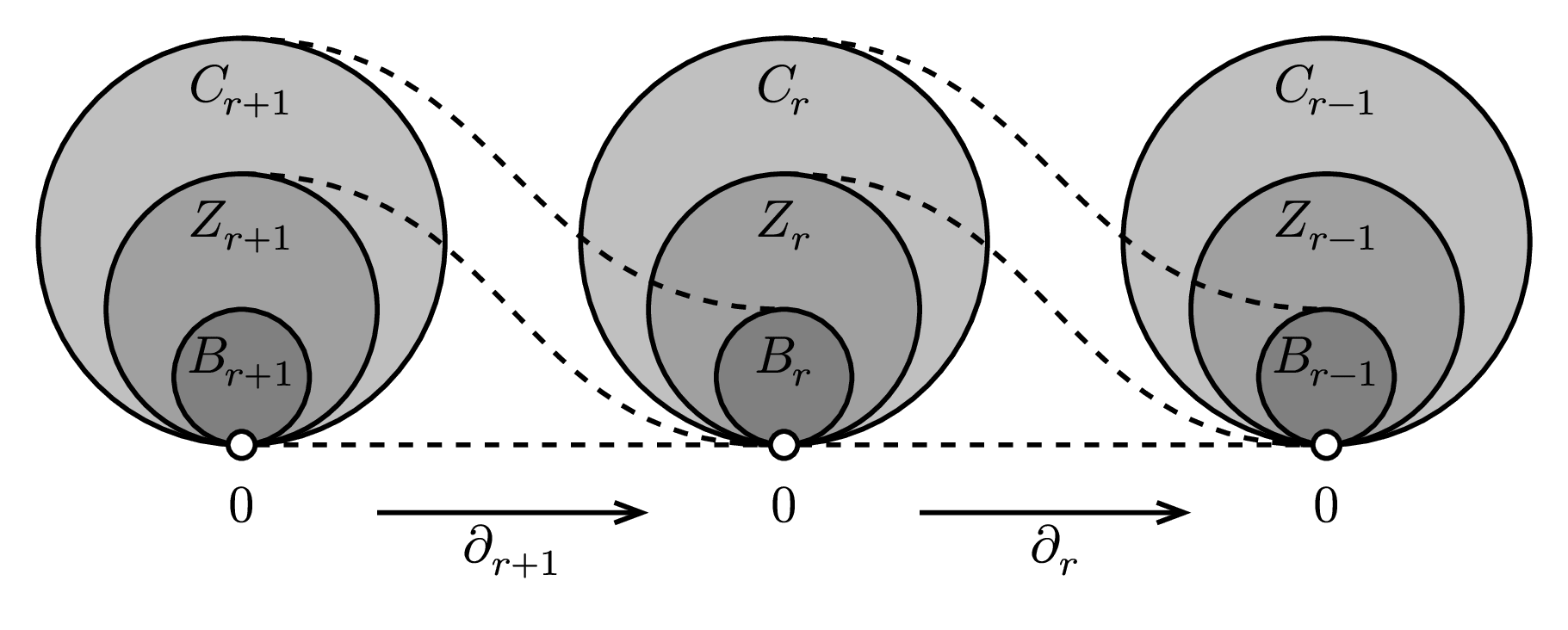
Diagram of a homology group $H_r$ of a chain complex. The boundary operator $\partial_r$ maps $r$ -chains to $(r-1)$ -chains, and its kernel is the group of $r$ -cycles $Z_r$ . The image of $\partial_{r+1}$ is the group of $r$ -boundaries $B_r$ . The homology group $H_r$ is defined as the quotient group $Z_r / B_r$ .

Download

PNG PDF SVG

Code

chain-homology.typ (61 lines)

// Ref. https://normaldeviate.wordpress.com/2012/07/01/topological-data-analysis/
#import "@preview/cetz:0.5.2": canvas, draw
#import draw: bezier, circle, content, line

#set page(width: auto, height: auto, margin: 8pt, fill: none)
#set text(size: 12pt)

#let dr = 0.1

#let stack(x, Cr, Zr, Br) = {
  let padding = 0.2
  for (name, radius, fill, label) in (
    ("C", 1.5, luma(192), Cr),
    ("Z", 1, luma(160), Zr),
    ("B", 0.5, luma(128), Br),
  ) {
    circle((x, 0), anchor: "south", radius: (radius, radius), fill: fill, name: name)
    content(name + ".north", label, anchor: "north", padding: padding)
  }

  circle((x, 0), anchor: "center", radius: dr, fill: rgb("#cdd3da"), name: "zero")
  content("zero.south", $0$, anchor: "north", padding: padding)
}

#canvas({
  let x = 4

  stack(0, $C_(r+1)$, $Z_(r+1)$, $B_(r+1)$)
  stack(x, $C_(r)$, $Z_(r)$, $B_(r)$)
  stack(2 * x, $C_(r-1)$, $Z_(r-1)$, $B_(r-1)$)

  let boundary-labels = ($partial_(r+1)$, $partial_(r)$)
  for span in range(2) {
    let offset = span * x
    let midpoint = offset + 0.5 * x
    line((offset + dr, 0), (offset + x - dr, 0), stroke: (dash: "dashed"))
    bezier(
      (offset, 2),
      (offset + x - dr, 0),
      (midpoint, 2),
      (midpoint, 0),
      stroke: (dash: "dashed"),
    )
    bezier(
      (offset, 3),
      (offset + x, 1),
      (midpoint, 3),
      (midpoint, 1),
      stroke: (dash: "dashed"),
    )
    let name = "arrow" + str(1 - span)
    line(
      (offset + 1, -0.5),
      (offset + x - 1, -0.5),
      mark: (end: "straight"),
      name: name,
    )
    content(name, boundary-labels.at(span), anchor: "north", padding: 0.1)
  }
})