Cylinder to Plane
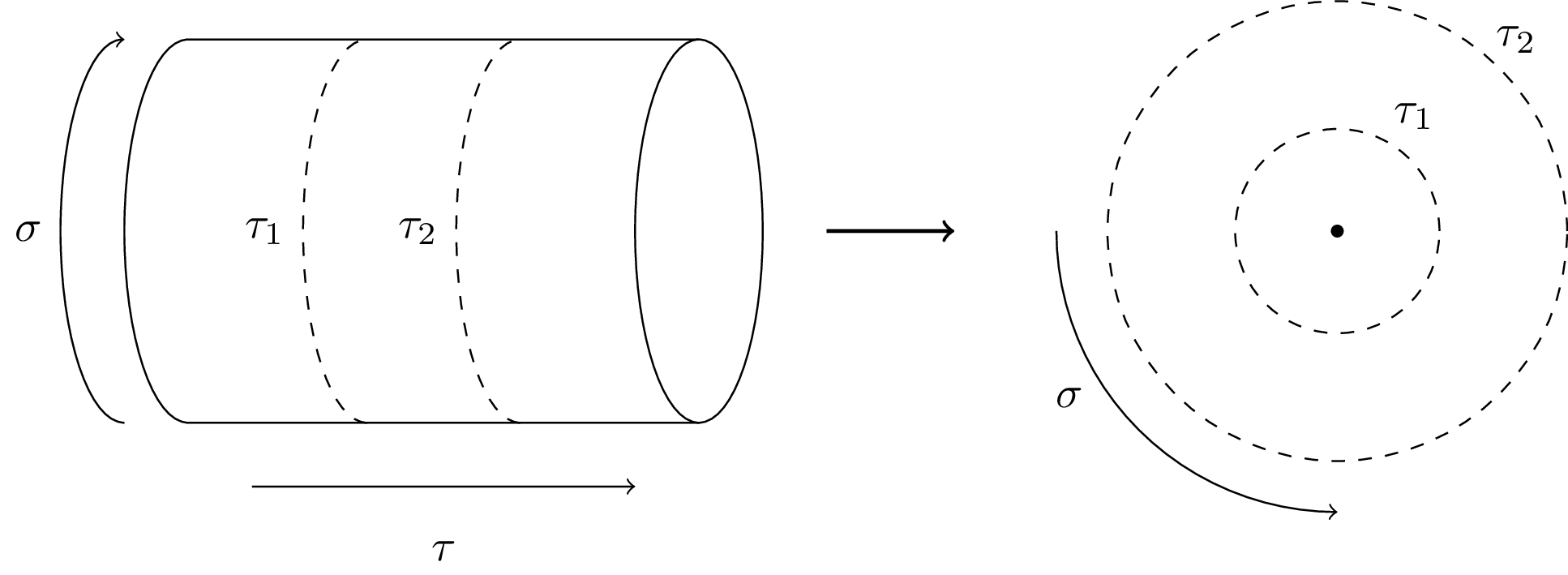
String theory: Primary fields and radial quantization A time-ordered product of fields on the cylinder maps to a radially ordered product in the complex plane. This graphic visualizes how different times on the cylinder correspond to different times on the plane.
Download
Code
LaTeX
cylinder-to-plane.tex (31 lines)
\documentclass[tikz]{standalone}
\begin{document}
\begin{tikzpicture}
\draw[dashed] (2.6,0) arc (-90:90:-0.5 and 1.5);% line 1
\draw[dashed] (1.4,0) arc (-90:90:-0.5 and 1.5);% line 2
\draw[->] (-0.5,0) arc (-90:90:-0.5 and 1.5);
\draw (0,0) -- (4,0);% bottom line
\draw (0,3) -- (4,3);% top line
\draw (0,0) arc (270:90:0.5 and 1.5);% left half of the left ellipse
\draw (4,1.5) ellipse (0.5 and 1.5);% right ellipse
\draw (0.6,1.5) node {$\tau_1$};
\draw (1.8,1.5) node {$\tau_2$};
\draw (-1.25,1.5) node {$\sigma$};
\draw[->] (0.5,-0.5) -- (3.5,-0.5);
\draw (2,-1) node {$\tau$};
\draw[->,thick] (5.0,1.5) -- (6,1.5);
\draw[dashed] (9,1.5) circle (0.8);
\draw[dashed] (9,1.5) circle (1.8);
\draw [->,domain=0:90] plot ({9 - 2.2*cos(\x)},{1.5-2.2*sin(\x)});
\draw (6.9,0.2) node {$\sigma$};
\draw (9.6,2.4) node {$\tau_1$};
\draw (10.4,3) node {$\tau_2$};
\node at (9,1.5) [circle,inner sep=1pt,fill=black] {};
\end{tikzpicture}
\end{document}