DFT Choices
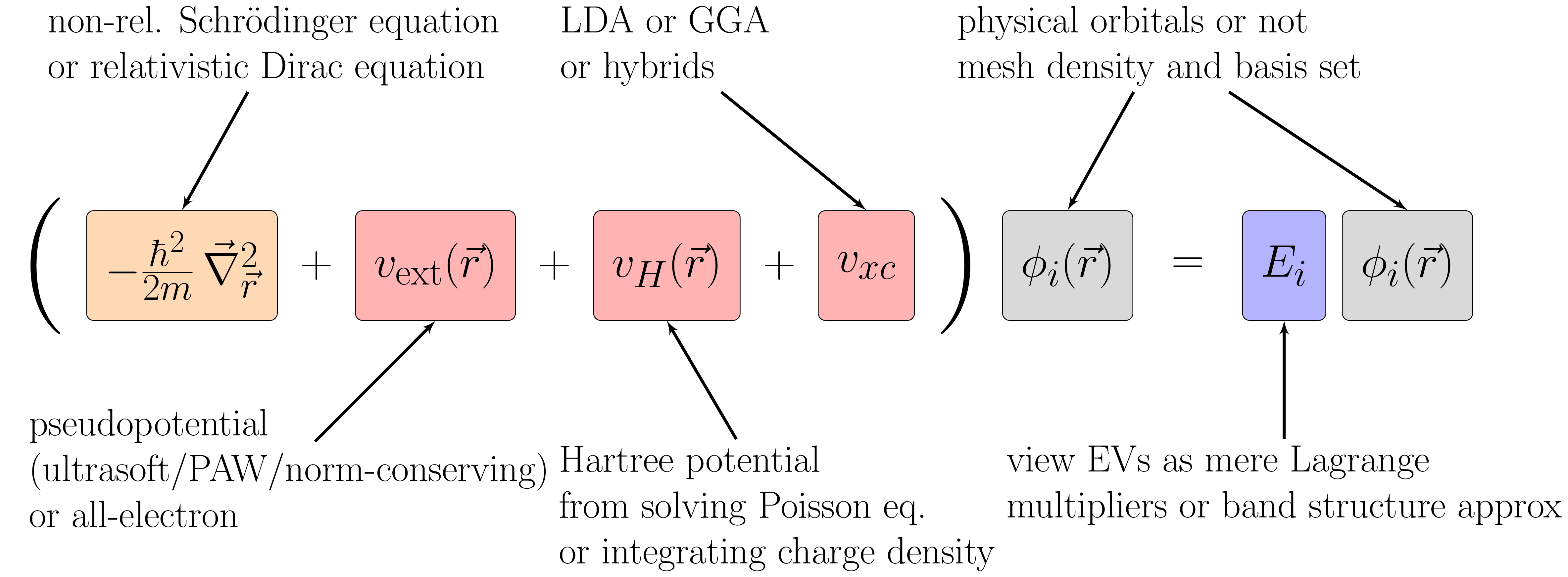
A diagram illustrating the various choices and components in density functional theory (DFT) calculations, including kinetic energy, external potential, Hartree potential, and exchange-correlation terms.
Download
Code
LaTeX
dft-choices.tex (44 lines)
\documentclass[tikz]{standalone}
\usetikzlibrary{positioning,arrows}
\begin{document}
\begin{tikzpicture}[
g/.style={rectangle,draw,rounded corners,minimum height=6em,inner sep=1em,font=\Huge},
w/.style={font=\Huge},
c/.style={node distance=15ex,align=left,font=\huge},
arrow/.style={draw,-latex',ultra thick}
]
\node [w,scale=3] (bra) {(};
\node [node distance=0ex,fill=orange!30,g,right=of bra] (kinetic) {$-\frac{\hbar^2}{2m}\,\vec{\nabla}_{\vec{r}}^2$};
\node [node distance=2ex,w,right=of kinetic] (plus1) {$+$};
\node [node distance=2ex,fill=red!30,g,right=of plus1] (external) {$v_\mathrm{ext}(\vec{r})$};
\node [node distance=2ex,w,right=of external] (plus2) {$+$};
\node [node distance=2ex,fill=red!30,g,right=of plus2] (hartree) {$v_H(\vec{r})$};
\node [node distance=2ex,w,right=of hartree] (plus3) {$+$};
\node [node distance=2ex,fill=red!30,g,right=of plus3] (xc) {$v_{xc}$};
\node [node distance=0ex,w,right=of xc,scale=3] (ket) {)};
\node [node distance=0ex,fill=gray!30,g,right=of ket] (phi1) {$\phi_i(\vec{r})$};
\node [node distance=4ex,w,right=of phi1] (equal) {$=$};
\node [node distance=4ex,fill=blue!30,g,right=of equal] (energy) {$E_i$};
\node [node distance=2ex,fill=gray!30,g,right=of energy] (phi2) {$\phi_i(\vec{r})$};
\node [c,above=of kinetic,xshift=5em] (kinetic comment) {non-rel. Schrödinger equation\\or relativistic Dirac equation};
\node [c,below=of external,xshift=-8em,yshift=2em] (external comment) {pseudopotential\\(ultrasoft/PAW/norm-conserving)\\or all-electron};
\node [c,below=of hartree,xshift=6em] (hartree comment) {Hartree potential\\from solving Poisson eq.\\or integrating charge density};
\node [c,above=of xc,xshift=-11em] (xc comment) {LDA or GGA\\or hybrids};
\node [c,above=of phi1,xshift=5em] (phi comment) {physical orbitals or not\\mesh density and basis set};
\node [c,below=of energy] (energy comment) {view EVs as mere Lagrange\\multipliers or band structure approx};
\path [arrow] (kinetic comment) -- (kinetic.north);
\path [arrow,shorten <=-3em] (external comment) -- (external.south);
\path [arrow] (hartree comment) -- (hartree.south);
\path [arrow] (xc comment) -- (xc.north);
\path [arrow] (phi comment) -- (phi1.north);
\path [arrow] (phi comment) -- (phi2.north);
\path [arrow] (energy comment) -- (energy.south);
\end{tikzpicture}
\end{document}
Typst
dft-choices.typ (152 lines)
#import "@preview/cetz:0.3.2": canvas, draw
#set page(width: auto, height: auto, margin: 8pt)
#set text(size: 15pt)
#canvas({
import draw: line, content, rect
// Define styles and constants
let node-sep = 1.7 // Reduced horizontal separation
let arrow-style = (mark: (end: "stealth", fill: black, offset: 4pt), stroke: 0.8pt)
let node-height = 1.6 // Shorter boxes
let node-width = 1.2 // Increased for larger text
// Helper function to create rounded rectangle nodes
let node(pos, text, fill: none, name: none, width: node-width, height: node-height) = {
rect(
(rel: (-width, -height / 2), to: pos),
(rel: (2 * width, height)),
fill: fill,
stroke: black + 0.4pt,
radius: 0.2,
name: name,
)
content(name, scale(140%, text))
}
// Create main equation nodes
node(
(0, 0),
$-frac(planck.reduce^2, 2m) arrow(nabla)_arrow(r)^2$,
fill: rgb("#ffd699"),
name: "kinetic",
width: 1.3 * node-width,
) // Kinetic term
content((rel: (-1.6 * node-width, 0.1), to: "kinetic"), scale(350%, $($), name: "lparen") // Opening parenthesis
content((rel: (1.6 * node-width, 0), to: "kinetic"), $+$, name: "plus-1")
node(
(rel: (1.4 * node-width, 0), to: "plus-1"),
$v_"ext" (arrow(r))$,
fill: rgb("#ffb3b3"),
name: "ext",
) // External potential
content((rel: (1.4 * node-width, 0), to: "ext"), $+$, name: "plus-2")
node(
(rel: (1.4 * node-width, 0), to: "plus-2"),
$v_H (arrow(r))$,
fill: rgb("#ffb3b3"),
name: "hartree",
) // Hartree potential
content((rel: (1.4 * node-width, 0), to: "hartree"), $+$, name: "plus-3")
node(
(rel: (1 * node-width, 0), to: "plus-3"),
$v_"xc"$,
fill: rgb("#ffb3b3"),
name: "xc",
width: .6 * node-width,
) // Exchange-correlation
content(
(rel: (1 * node-width, 0.1), to: "xc"),
scale(350%, $)$),
name: "rparen",
padding: 5pt,
) // Large closing parenthesis
node(
(rel: (2.4 * node-width, 0), to: "xc"),
$phi_i (arrow(r))$,
fill: rgb("#e6e6e6"),
name: "phi1",
) // Wavefunction 1
content((rel: (1.4 * node-width, 0), to: "phi1"), $=$, name: "eq-1")
node(
(rel: (1 * node-width, 0), to: "eq-1"),
$E_i$,
fill: rgb("#b3d9ff"),
name: "energy",
width: 0.6 * node-width,
) // Energy
node(
(rel: (1.9 * node-width, 0), to: "energy"),
$phi_i (arrow(r))$,
fill: rgb("#e6e6e6"),
name: "phi2",
) // Wavefunction 2
// Add comment boxes and arrows
let comment(pos, text, target-name, name: none) = {
content(pos, align(center, text), name: name)
line(name, target-name, ..arrow-style)
}
// Add comments with arrows
comment(
(node-sep, 3),
[non-rel. Schrödinger equation\
or relativistic Dirac equation],
"kinetic",
name: "kinetic-comment",
)
comment(
(rel: (-2, -3), to: "ext"),
[pseudopotential\
(ultrasoft/PAW/norm-conserving)\ or all-electron],
"ext",
name: "ext-comment",
)
comment(
(4.9 * node-sep, -3),
[Hartree potential\ from solving Poisson eq.\
or integrating charge density],
"hartree",
name: "hartree-comment",
)
comment(
(5 * node-sep, 3),
[LDA or GGA\ or hybrids],
"xc",
name: "xc-comment",
)
comment(
(rel: (2, 3), to: "phi1"),
[physical orbitals or not\ mesh density and basis set],
"phi1",
name: "phi-comment",
)
line("phi-comment", "phi2", ..arrow-style)
comment(
(rel: (0, -3), to: "energy"),
[view EVs as mere Lagrange\ multipliers or band structure approx],
"energy",
name: "energy-comment",
)
})