Feynman Diagram One Point

physicsquantum field theoryrenormalizationcetztikz

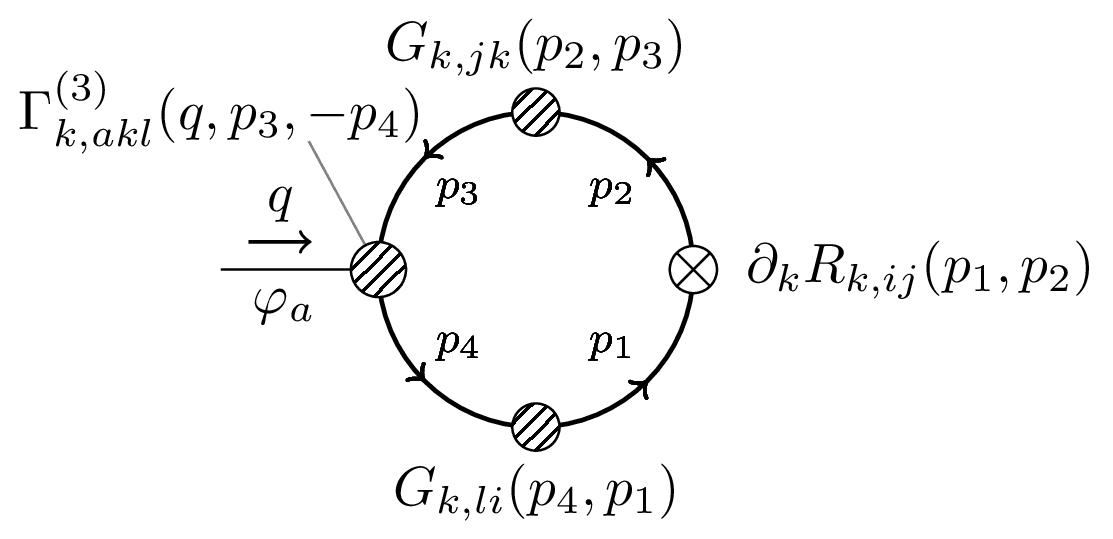
This Feynman diagram corresponds to the integrand in this expression for $\displaystyle \partial_t \Gamma_{k,a}^{(1)}(q) = -\frac{1}{2} \sum_{\substack{i,j\\k,l}}^N \int_{\substack{p_1,p_2\\p_3^\prime,p_4^\prime}} \frac{\partial_t R_{k,ij}(p_1,p_2)}{\Gamma_{k,jk}^{(2)}(p_2,p_3) + R_{k,jk}(p_2,p_3)} \, \frac{\Gamma_{k,akl}^{(3)}(q,p_3,p_4)}{\Gamma_{k,li}^{(2)}(p_4,p_1) + R_{k,li}(p_4,p_1)}.$

Download

PNG PDF SVG

Code

LaTeX

feynman-diagram-one-point.tex (39 lines)

\documentclass[tikz]{standalone}

\usetikzlibrary{patterns,decorations.markings}

\tikzset{
    cross/.style={fill=white,path picture={\draw[black]
        (path picture bounding box.south east) -- (path picture bounding box.north west)
        (path picture bounding box.south west) -- (path picture bounding box.north east);}},
    dressed/.style={fill=white,postaction={pattern=north east lines}},
    momentum/.style={->,semithick,yshift=5pt,shorten >=5pt,shorten <=5pt},
    loop/.style 2 args={thick,decoration={markings,mark=at position {#1} with {\arrow{>},\node[anchor=\pgfdecoratedangle-90,font=\footnotesize] {$p_{#2}$};}},postaction={decorate}},
    label/.style={thin,gray,shorten <=-1.5ex}
}

\def\lrad{1}
\def\mrad{0.175*\lrad}
\def\srad{0.15*\lrad}

\begin{document}
\begin{tikzpicture}[pin edge={shorten <=5*\lrad}]

  % Loop
  \draw[loop/.list={{0.125}{2},{0.125*3}{3},{0.125*5}{4},{0.125*7}{1}}] (0,0) circle (\lrad);
  \draw[cross] (\lrad,0) circle (\srad) node[right=6pt] {$\partial_k R_{k,ij}(p_1,p_2)$};
  \draw[dressed] (0,\lrad) circle (\srad) node[above=3pt] {$G_{k,jk}(p_2,p_3)$};
  \draw[dressed] (0,-\lrad) circle (\srad) node[below=3pt] {$G_{k,li}(p_4,p_1)$};

  % External line
  \draw (-2*\lrad,0) -- (-\lrad,0) node[pos=0.4,below] {$\varphi_a$};
  \draw[momentum] (-2*\lrad,0) -- (-1.25*\lrad,0) node[midway,above] {$q$};

  % Vertex
  \node (Gkakl) at (-2*\lrad,\lrad) {$\Gamma_{k,akl}^{(3)}(q,p_3,-p_4)$};
  \draw[label] (Gkakl.-30) -- (-\lrad,0);
  \draw[dressed] (-\lrad,0) circle (\mrad);

\end{tikzpicture}
\end{document}

Typst

feynman-diagram-one-point.typ (121 lines)

#import "@preview/cetz:0.3.4": canvas, draw
#import "@preview/modpattern:0.1.0": modpattern
#import draw: line, content, circle, mark

#set page(width: auto, height: auto, margin: 8pt)

// Constants
#let radius = 1.2 // Increased for better spacing
#let med-rad = 0.175 * radius // \mrad
#let small-rad = 0.15 * radius // \srad

// Styles
#let arrow-style = (
  mark: (end: "stealth", fill: black, scale: .5),
  stroke: (thickness: 0.75pt),
)
#let label-style = (stroke: gray + 0.3pt)
#let hatched = modpattern(
  (.1cm, .1cm),
  std.line(start: (0%, 100%), end: (100%, 0%), stroke: 0.5pt),
  background: white,
)

// Helper functions
#let cross(pos, label: none, rel-label: (6pt, 0), name: none, ..rest) = {
  let txt = text(size: 16pt, baseline: -0.25pt)[$times.circle$]
  content(pos, txt, stroke: none, fill: white, frame: "circle", padding: -2.7pt, name: name, ..rest)
  if label != none {
    content((rel: rel-label, to: pos), $#label$, anchor: "west")
  }
}

#let dressed-vertex(pos, label: none, rel-label: (3pt, 0), name: none, radius: small-rad, ..rest) = {
  circle(pos, radius: radius, fill: hatched, name: name, stroke: 0.5pt)
  if label != none {
    let label-pos = if rel-label != none { (rel: rel-label, to: pos) } else { pos }
    content(label-pos, $#label$, ..rest)
  }
}

#canvas({
  // Main loop with momentum labels
  circle((0, 0), radius: radius, stroke: 1pt, name: "loop")

  // Add momentum arrows and labels around loop
  for (ii, pos) in ((2, "0.125"), (3, "0.375"), (4, "0.625"), (1, "0.875")) {
    let angle = float(pos) * 360
    let label-angle = (angle - 3) * 1deg

    // Add momentum labels
    let rel-pos = (0.6 * radius * calc.cos(label-angle), 0.6 * radius * calc.sin(label-angle))
    content(
      (rel: rel-pos, to: "loop"),
      $p_#ii$,
      size: 8pt,
    )

    // Add arrow marks
    mark(
      symbol: "stealth",
      (name: "loop", anchor: angle * 1deg),
      (name: "loop", anchor: (angle + 1) * 1deg),
      ..(width: .25, length: .15, stroke: .7pt, angle: 60deg, scale: .7, fill: black),
    )
  }

  // Add vertices with labels
  cross(
    (radius, 0),
    label: $partial_k R_(k,i j)(p_1,p_2)$,
    rel-label: (0.3, 0),
    name: "regulator",
  )

  dressed-vertex(
    (0, radius),
    label: $G_(k,j k)(p_2,p_3)$,
    rel-label: (0, 0.3),
    name: "vertex-top",
  )

  dressed-vertex(
    (0, -radius),
    label: $G_(k,l i)(p_4,p_1)$,
    rel-label: (0, -0.3),
    name: "vertex-bottom",
  )

  // External line
  line((-2.5 * radius, 0), (-radius, 0), stroke: 1pt, name: "external")
  content((rel: (-0.6 * radius, -0.3), to: "external"), $phi_a$)

  // External momentum arrow
  line(
    (-2.3 * radius, 0.15),
    (-1.5 * radius, 0.15),
    ..arrow-style,
    name: "q-arrow",
  )
  content((rel: (0, 0.3), to: "q-arrow.mid"), $q$)

  // Vertex label with connecting line
  content(
    (-2.2 * radius, 1.2 * radius),
    $Gamma_(k,a k l)^((3))(q,p_3,-p_4)$,
    name: "gamma-label",
  )
  line(
    "gamma-label",
    (-radius, 0),
    ..label-style,
  )

  // Dressed vertex at external line connection
  dressed-vertex(
    (-radius, 0),
    radius: med-rad,
    name: "vertex-external",
  )
})