Isotherms

physicsthermodynamicsstatistical mechanicscetztikz

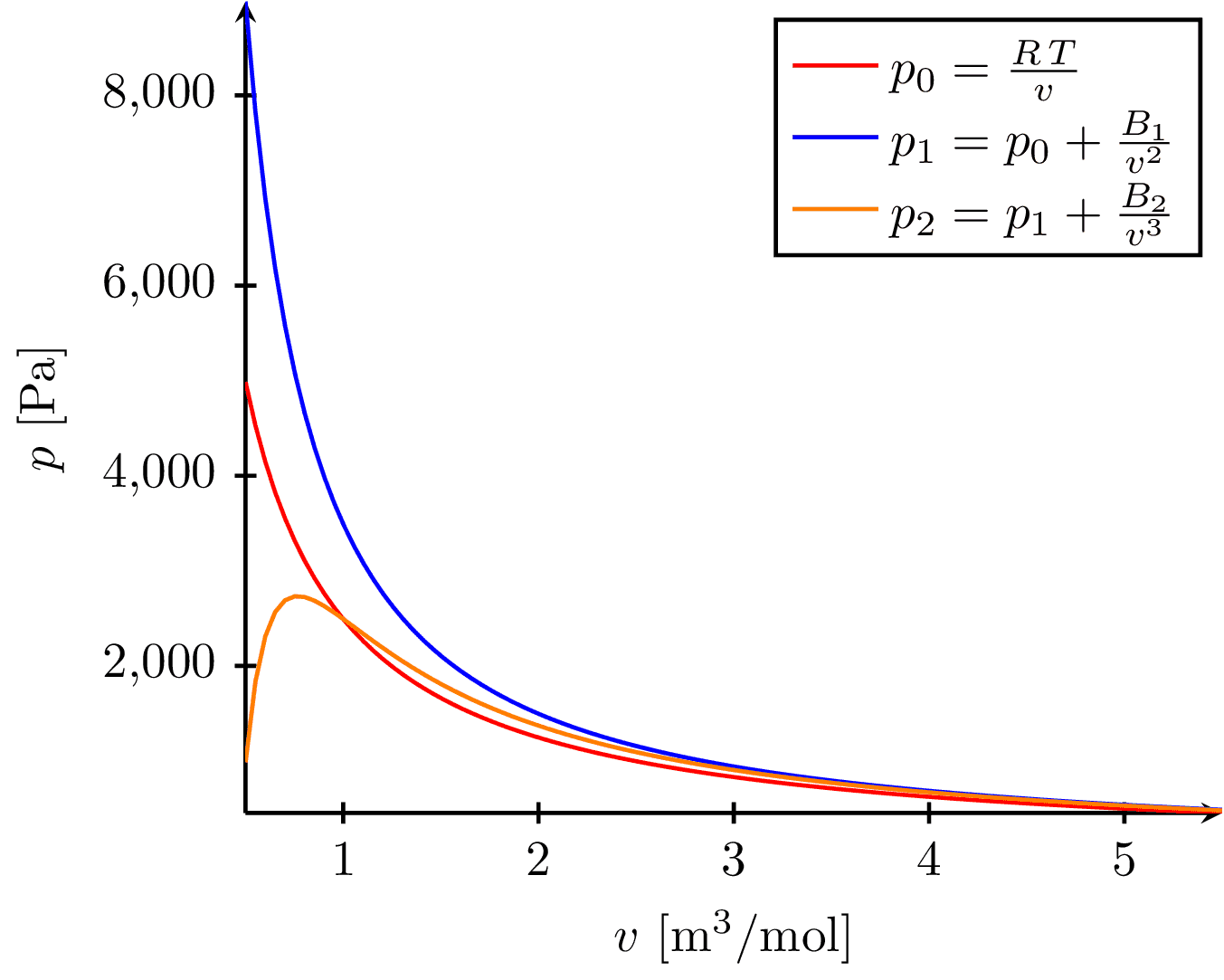
This image visualizes the behavior of gas isotherms (curves showing pressure-volume relationships at constant temperature), represented by three equations of state, as a function of volume. The equations include the ideal gas law, and two other modified laws accounting for molecular interactions. The x-axis represents the molar volume and the y-axis represents the pressure of the gas.