Matsubara Contour 1
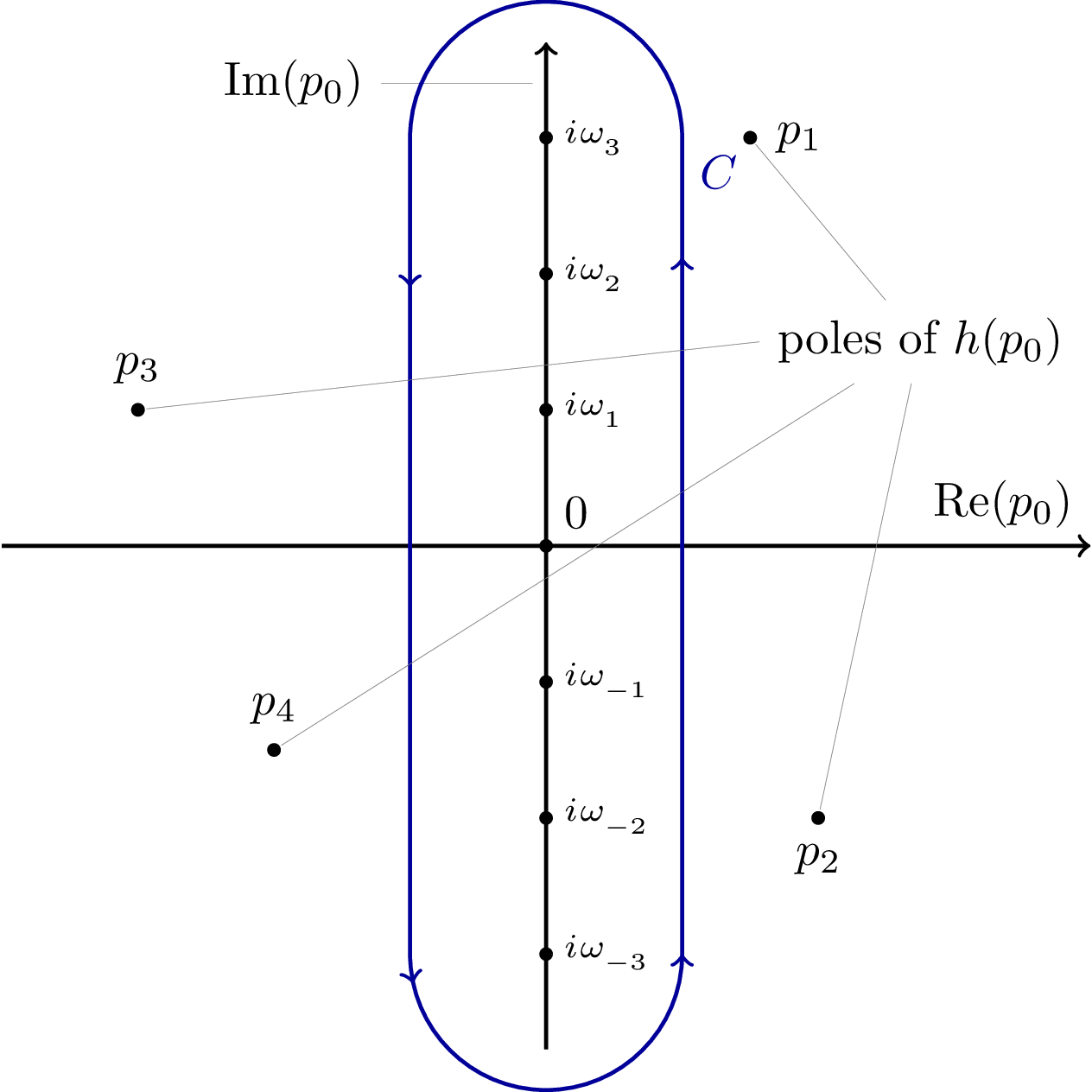
Initial contour C for evaluating Matsubara frequency sums. C runs counterclockwise around the imaginary p₀-axis where the Matsubara frequencies ωₙ = 2πn/β lie, but excludes the poles of the propagator 1/(-p₀² + x²). The integrand includes the Bose-Einstein distribution which has simple poles at all Matsubara frequencies with residue T.
Download
Code
LaTeX
matsubara-contour-1.tex (47 lines)
\documentclass[tikz]{standalone}
\usepackage{mathtools}
\let\Im\relax
\DeclareMathOperator{\Im}{Im}
\let\Re\relax
\DeclareMathOperator{\Re}{Re}
\usetikzlibrary{decorations.markings,positioning}
\providecommand{\poles}{
\node (poles) at (2.75,1.5) {poles of $h(p_0)$};
\draw[fill]
(1.5,3) coordinate [circle,fill,inner sep=1pt,label=right:$p_1$] (p1)
(2,-2) coordinate [circle,fill,inner sep=1pt,label=below:$p_2$] (p2)
(-3,1) coordinate [circle,fill,inner sep=1pt,label=above:$p_3$] (p3)
(-2,-1.5) coordinate [circle,fill,inner sep=1pt,label=above:$p_4$] (p4);
\draw[ultra thin,gray] (poles) -- (p1) (poles) -- (p2) (poles.west) -- (p3) (poles) -- (p4);
}
\def\xr{3}
\def\yr{3}
\begin{document}
\begin{tikzpicture}[thick]
% Axes
\draw [->] (-\xr-1,0) -- (\xr+1,0) node [above left] {$\Re(p_0)$};
\draw [->] (0,-\yr-0.7) -- (0,\yr+0.7) coordinate [below left = 0.3 and 0.1] (y-axis);
\node (y-label) at ([xshift=-50]y-axis) {$\Im(p_0)$};
\draw[ultra thin,gray] (y-axis) -- (y-label);
% Matsubara frequencies
\foreach \n in {-\yr,...,-1,1,2,...,\yr}{%
\draw[fill] (0,\n) circle (1pt) node [right,font=\scriptsize] {$i \mkern1mu \omega_{_{\n}}$};}
\draw[fill] (0,0) circle (1pt) node [above right] {0};
% Contour line
\draw[blue!60!black,decoration={markings,mark=between positions 0 and 1 step 0.28 with \arrow{>}},postaction={decorate}] (1,-\yr) -- (1,\yr) node [below right] {$C$} arc (0:180:1) (-1,\yr) -- (-1,-\yr) arc (180:360:1);
% Poles of h(p_0)
\poles
\end{tikzpicture}
\end{document}
Typst
matsubara-contour-1.typ (119 lines)
#import "@preview/cetz:0.3.4": canvas, draw
#import draw: line, content, circle, arc, set-style
#set page(width: auto, height: auto, margin: 8pt)
// Constants
#let x-range = 3
#let y-range = 3
// Define styles
#let arrow-style = (
mark: (end: "stealth", fill: black, scale: 0.5),
stroke: 0.5pt,
)
#let dark-blue = blue.darken(20%)
// Helper function to draw poles
#let draw-poles(poles-label-pos) = {
// Draw poles label and connecting lines
content(poles-label-pos, [poles of $h(p_0)$], name: "poles-label")
// Draw the poles
circle((1.5, 3), radius: 0.05, fill: black, name: "p1")
circle((2, -2), radius: 0.05, fill: black, name: "p2")
circle((-3, 1), radius: 0.05, fill: black, name: "p3")
circle((-2, -1.5), radius: 0.05, fill: black, name: "p4")
// Add pole labels
content("p1", $p_1$, anchor: "west", padding: 2pt)
content("p2", $p_2$, anchor: "north", padding: 2pt)
content("p3", $p_3$, anchor: "south", padding: 2pt)
content("p4", $p_4$, anchor: "north", padding: 2pt)
// Connect poles to label with thin gray lines
let stroke = (stroke: (paint: gray, thickness: 0.2pt))
line("poles-label", "p1", ..stroke)
line("poles-label", "p2", ..stroke)
line("poles-label.west", "p3", ..stroke)
line("poles-label", "p4", ..stroke)
}
#canvas({
// Draw axes
line((-x-range - 1, 0), (x-range + 1, 0), ..arrow-style, name: "x-axis")
content("x-axis.end", $"Re"(p_0)$, anchor: "south-east", padding: 2pt)
line((0, -y-range - 0.7), (0, y-range + 0.7), ..arrow-style, name: "y-axis")
content((rel: (-1, 0), to: "y-axis.95%"), $"Im"(p_0)$, name: "y-label", anchor: "south-east", padding: 2pt)
line("y-axis.98%", "y-label", stroke: (paint: gray, thickness: 0.2pt))
// Draw Matsubara frequencies
for n in range(-y-range, y-range + 1) {
if n != 0 {
circle((0, n), radius: 0.03, fill: black, name: "freq-" + str(n))
content(
"freq-" + str(n),
$i omega_#text(size: 0.7em)[#n]$,
anchor: "west",
padding: (x: 3pt),
)
}
}
// Draw origin
circle((0, 0), radius: 0.03, fill: black, name: "origin")
content("origin", [0], anchor: "south-west", padding: (left: 3pt, bottom: 2pt))
// Draw contour line
// Right vertical line
// Base line with name
line(
(1, -y-range - 0.3),
(1, y-range + 0.3),
stroke: dark-blue,
mark: (end: "stealth", scale: 0.5),
name: "right-line",
)
// Top semicircle - positioned to fully enclose the y-axis
arc(
(0, y-range + 0.6),
radius: 1,
start: 0deg,
stop: 180deg,
stroke: dark-blue,
mark: (end: "stealth", scale: 0.5),
name: "top-arc",
anchor: "center",
)
// Left vertical line
line(
(-1, y-range + 0.3),
(-1, -y-range - 0.3),
stroke: dark-blue,
name: "left-line",
mark: (end: "stealth", scale: 0.5),
)
// Bottom semicircle - positioned to fully enclose the y-axis
arc(
(0, -y-range - 0.5),
radius: 1,
start: 180deg,
stop: 360deg,
stroke: dark-blue,
mark: (end: "stealth", scale: 0.5),
name: "bottom-arc",
anchor: "center",
)
// Add contour label
content("right-line.end", text(fill: dark-blue)[$C$], anchor: "south-west", padding: 2pt)
// Draw poles
draw-poles((2.75, 1.5))
})