Matsubara Contour 3
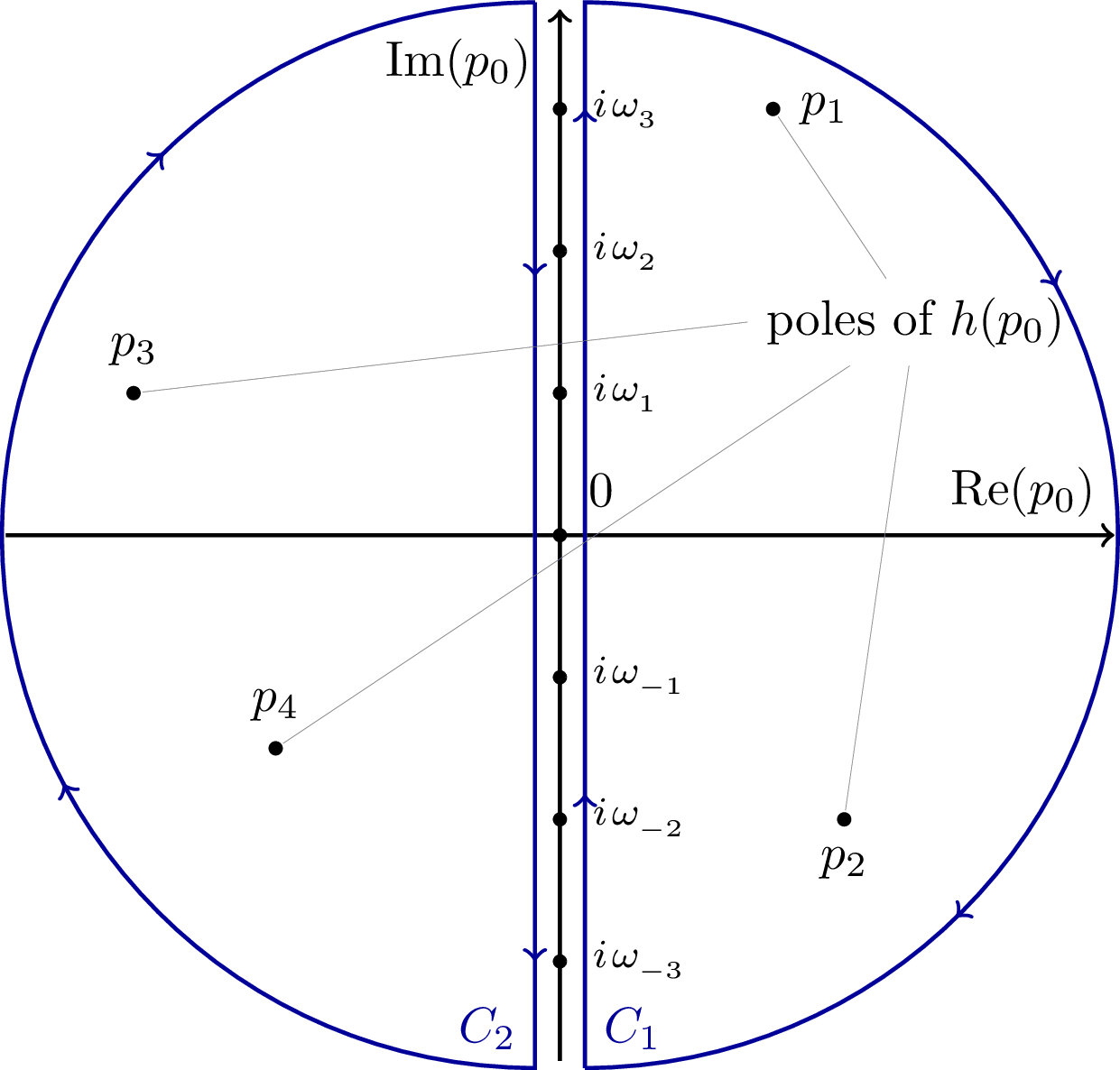
Second deformation of the Matsubara contour where the small circles C₁ and C₂ are expanded to enclose the entire complex plane except for the imaginary axis. This contour picks up both pole and branch cut contributions from the propagator, with the branch cuts arising from the sign function s(p₀).
Download
Code
LaTeX
matsubara-contour-3.tex (48 lines)
\documentclass[tikz]{standalone}
\usepackage{mathtools}
\let\Im\relax
\DeclareMathOperator{\Im}{Im}
\let\Re\relax
\DeclareMathOperator{\Re}{Re}
\usetikzlibrary{decorations.markings,positioning}
\providecommand{\poles}{
\node (poles) at (2.5,1.5) {poles of $h(p_0)$};
\draw[fill]
(1.5,3) coordinate [circle,fill,inner sep=1pt,label=right:$p_1$] (p1)
(2,-2) coordinate [circle,fill,inner sep=1pt,label=below:$p_2$] (p2)
(-3,1) coordinate [circle,fill,inner sep=1pt,label=above:$p_3$] (p3)
(-2,-1.5) coordinate [circle,fill,inner sep=1pt,label=above:$p_4$] (p4);
\draw[ultra thin,gray] (poles) -- (p1) (poles) -- (p2) (poles.west) -- (p3) (poles) -- (p4);
}
\def\xr{3.5}
\def\yr{3}
\begin{document}
\begin{tikzpicture}[thick]
% Axes
\draw[->] (-\xr-0.4,0) -- (\xr+0.4,0) node [above left] {$\Re(p_0)$};
\draw[->] (0,-\yr-0.7) -- (0,\yr+0.7) node[below left=0.1] {$\Im(p_0)$};
% Matsubara frequencies
\foreach \n in {-\yr,...,-1,1,2,...,\yr}{%
\draw[fill] (0,\n) circle (1pt) node [right=0.1,font=\footnotesize] {$i \mkern2mu \omega_{_{\n}}$};}
\draw[fill] (0,0) circle (1pt) node [above right=0.1] {0};
% Right contour line
\draw[xshift=5,blue!60!black,decoration={markings,mark=between positions 0.1 and 1 step 0.25 with \arrow{>}},postaction={decorate}] (0,-\yr-0.75) node [above right] {$C_1$} -- (0,\yr+0.75) arc (90:-90:\yr+0.75);
% Left contour line
\draw[xshift=-5,blue!60!black,decoration={markings,mark=between positions 0.1 and 1 step 0.25 with \arrow{>}},postaction={decorate}] (0,\yr+0.75) -- (0,-\yr-0.75) node [above left] {$C_2$} arc (270:90:\yr+0.75);
% Poles
\poles
\end{tikzpicture}
\end{document}
Typst
matsubara-contour-3.typ (121 lines)
#import "@preview/cetz:0.3.4": canvas, draw
#import draw: line, content, circle, arc, set-style
#set page(width: auto, height: auto, margin: 8pt)
// Constants
#let x-range = 3
#let y-range = 3
#let main-radius = y-range + 1.5
#let pole-radius = 0.5
#let dot-radius = 0.05
#let small-dot-radius = 0.03
#let y-offset = 0.25
// Styles
#let arrow-style = (mark: (end: "stealth", scale: 0.5))
#let dark-blue = blue.darken(20%)
#let marc-style = (symbol: "stealth", fill: dark-blue, scale: 0.5, shorten-to: none)
#let gray-line = (paint: gray, thickness: 0.2pt)
#let contour-style = (paint: dark-blue, thickness: 0.8pt)
// Helper function to draw poles
#let draw-poles(poles-label-pos) = {
content(poles-label-pos, [poles of $h(p_0)$], name: "poles-label")
// Pole positions: (x, y, name, anchor)
let pole-positions = (
(1.5, 3, "p1", "west"),
(2, -2, "p2", "north"),
(-3, 1, "p3", "south"),
(-2, -1.5, "p4", "north"),
)
for (x, y, name, anchor) in pole-positions {
circle((x, y), radius: dot-radius, fill: black, name: name)
content(name, $p_#name.last()$, anchor: anchor, padding: 2pt)
let connect-point = if name == "p3" { "poles-label.west" } else { "poles-label" }
line(connect-point, name, stroke: gray-line)
}
}
// Helper function to draw a semicircle with arrows
#let draw-semicircle(center-x, start-angle, end-angle, name) = {
arc(
(center-x, 0),
radius: main-radius,
start: start-angle,
stop: end-angle,
stroke: contour-style,
mark: (
end: (
(pos: 25%, ..marc-style),
(pos: 50%, ..marc-style),
(pos: 75%, ..marc-style),
),
),
name: name,
anchor: "origin",
)
}
// Helper function to draw a vertical line with arrows
#let draw-vertical-line(x, start-y, end-y, name) = {
line(
(x, start-y),
(x, end-y),
stroke: contour-style,
mark: (
end: (
(pos: 25%, ..marc-style),
(pos: 50%, ..marc-style),
(pos: 75%, ..marc-style),
),
),
name: name,
)
}
#canvas({
// Draw axes
line((-main-radius - y-offset, 0), (main-radius + y-offset, 0), ..arrow-style, name: "x-axis")
content("x-axis.end", $"Re"(p_0)$, anchor: "south-east", padding: 2pt)
line((0, -main-radius), (0, main-radius), ..arrow-style, name: "y-axis")
content("y-axis.97%", $"Im"(p_0)$, anchor: "north-east", padding: (right: 8pt))
// Draw Matsubara frequencies
for n in range(-y-range, y-range + 1) {
if n != 0 {
circle((0, n), radius: small-dot-radius, fill: black, name: "freq-" + str(n))
content(
"freq-" + str(n),
$i omega_#text(size: 0.7em)[#n]$,
anchor: "west",
padding: (left: 10pt),
)
}
}
// Draw origin
circle((0, 0), radius: small-dot-radius, fill: black, name: "origin")
content("origin", [0], anchor: "south-west", padding: (left: 10pt, bottom: 3pt))
// Draw split contour
// Right half (C₁): vertical line down + right semicircle
draw-vertical-line(y-offset, main-radius, -main-radius, "right-line")
draw-semicircle(y-offset, -90deg, 90deg, "right-arc")
// Left half (C₂): vertical line up + left semicircle
draw-vertical-line(-y-offset, -main-radius, main-radius, "left-line")
draw-semicircle(-y-offset, 90deg, 270deg, "left-arc")
// Add contour labels
content("right-line.end", text(fill: dark-blue)[$C_1$], anchor: "south-west", padding: 4pt)
content("left-line.start", text(fill: dark-blue)[$C_2$], anchor: "south-east", padding: 4pt)
// Draw poles
draw-poles((2.5, 1.5))
})