« home

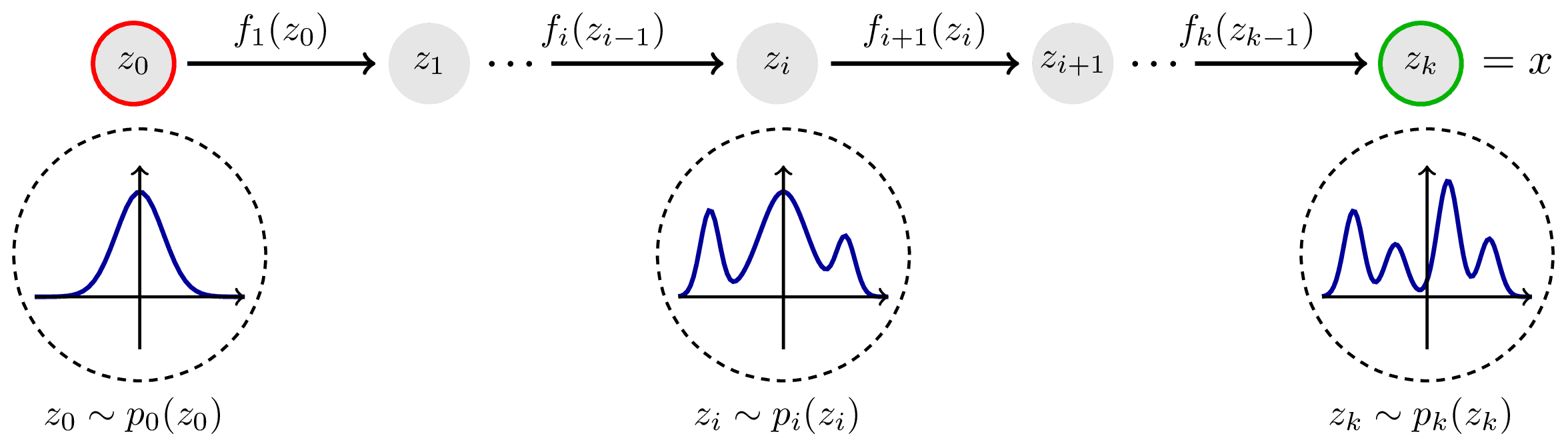
Normalizing Flow

machine learninggenerative modelingprobabilitynormalizing flowscetztikz

A chain of bijections f=f1∘⋯∘fkf = f_1 \circ \dots \circ f_k constituting a normalizing flow which step by step transforms a simple distribution p0(z⃗0)p_0(\vec z_0) into a complex one pk(z⃗k)p_k(\vec z_k). The bijections are trained to fit pk(z⃗k)p_k(\vec z_k) to some target distribution px(x⃗)p_x(\vec x). Inspired by Lilian Weng.


Normalizing Flow

  Download

PNGPDFSVG

  Code

  LaTeX

normalizing-flow.tex (39 lines)

\documentclass[tikz]{standalone}

\usetikzlibrary{positioning}

\newcommand{\distro}[4][40]{
  \begin{tikzpicture}[thick]
    \draw[dashed, dash pattern={on 2.3 off 2}] (0, .4) circle (12mm);
    \draw[blue!60!black, very thick] plot[variable=\t, domain=-1:1, samples=#1] ({\t}, {#2 * exp(-10*(\t)^2) + #3 * exp(-60*(\t-0.6)^2 - \t) + #3 * exp(-60*(\t+0.7)^2 - 0.2) + #4 * 0.5 * exp(-50*(\t+0.3)^2) + #4 * exp(-50*(\t-0.2)^2 + 0.1)});
    \draw[solid, ->] (-1, 0)--(1, 0);
    \draw[solid, ->] (0, -0.5)--(0, 1.25);
  \end{tikzpicture}
}

\begin{document}
\begin{tikzpicture}[
    node distance=2, very thick,
    flow/.style={shorten >=3, shorten <=3, ->},
    znode/.style={circle, fill=black!10, minimum size=22, inner sep=0},
  ]

  \node[znode, draw=red] (z0) {$z_0$};
  \node[znode, right=of z0] (z1) {$z_1$};
  \draw[flow] (z0) -- node[above, midway] {$f_1(z_0)$} (z1);

  \node[znode, right=2.5 of z1] (zi) {$z_i$};
  \node[znode, right=of zi] (zip1) {$z_{i+1}$};
  \draw[flow] (zi) -- node[above, midway] {$f_{i+1}(z_i)$} (zip1);
  \draw[flow, shorten <=5ex] (z1) -- node[pos=0.16, inner sep=1] {\textbf\dots} node[above, midway] {$f_i(z_{i-1})$} (zi);

  \node[znode, draw=green!70!black, right=2.5 of zip1] (zk) {$z_k$};
  \draw[flow, shorten <=5ex] (zip1) -- node[pos=0.16, inner sep=1] {\textbf\dots} node[above, midway] {$f_k(z_{k-1})$} (zk);
  \node[right=0 of zk, scale=1.2] {$= x$};
  \node[outer sep=0, inner sep=0, below=0.2 of z0, label={below:$z_0 \sim p_0(z_0)$}] (f0) {\distro{1}{0}{0}};
  \node[outer sep=0, inner sep=0, below=0.2 of zi, label={below:$z_i \sim p_i(z_i)$}] (fi) {\distro[70]{1}{1}{0}};
  \node[outer sep=0, inner sep=0, below=0.2 of zk, label={below:$z_k \sim p_k(z_k)$}] (fk) {\distro[90]{0}{1}{1}};

\end{tikzpicture}
\end{document}

  Typst

normalizing-flow.typ (104 lines)

#import "@preview/cetz:0.3.2": canvas, draw
#import "@preview/cetz-plot:0.1.1": plot
#import draw: line, content, circle, group, translate

#set page(width: auto, height: auto, margin: 8pt)

// Helper functions for probability distributions
#let gaussian(x, mu: 0, sigma: 0.2) = (
  (1 / (sigma * calc.sqrt(2 * calc.pi))) * calc.exp(-0.5 * calc.pow((x - mu) / sigma, 2))
)

#let mixture(x, params) = {
  let sum = 0
  for (weight, mu, sigma) in params {
    sum += weight * gaussian(x, mu: mu, sigma: sigma)
  }
  return sum
}

// Distribution functions
#let p0(x) = 0.55 * gaussian(x, mu: 0, sigma: 0.2)
#let pi(x) = mixture(x, ((0.6, -0.3, 0.2), (0.4, 0.4, 0.25)))
#let pk(x) = mixture(x, ((0.4, -0.4, 0.15), (0.3, 0, 0.12), (0.3, 0.4, 0.15)))

// Helper function to draw distribution plots
#let draw-distro(x, y, dist-fn, name: none) = {
  // Draw circle outline
  circle((x, y + 0.3), radius: 1, stroke: (dash: "dashed"), name: name)

  // Draw coordinate axes
  line((x - 0.8, y), (x + 0.8, y), mark: (end: ">", scale: 0.5, fill: black))
  line((x, y - 0.5), (x, y + 1.1), mark: (end: ">", scale: 0.5, fill: black))

  let plot-size = (1.6, 1.1)

  group({
    translate((x - 0.8, y))
    plot.plot(
      size: plot-size,
      axis-style: none,
      y-min: 0,
      y-max: 1.5,
      {
        plot.add(style: (stroke: blue.darken(20%) + 1.2pt), domain: (-0.8, 0.8), samples: 100, dist-fn)
      },
    )
  })
}

#canvas({
  // Constants for layout
  let node-spacing = 3
  let y-base = 0
  let y-distro = y-base - 2 // vertical offset for distributions

  // Helper function for z-nodes
  let z-node(x, label, special: none, name: none, ..rest) = {
    circle(
      fill: gray.transparentize(70%),
      (x, y-base),
      radius: 0.4,
      stroke: if special != none { special } else { none },
      name: name,
    )
    content(name, label, ..rest)
  }

  // Draw all nodes first
  z-node(0, $z_0$, special: red, name: "z0")
  z-node(node-spacing, $z_1$, name: "z1")
  z-node(2 * node-spacing, $z_i$, name: "zi")
  z-node(3 * node-spacing, $z_(i+1)$, name: "zi1")
  z-node(4 * node-spacing, $z_k$, special: rgb("#2d862d"), name: "zk")

  // Then add dots
  content((rel: (0.7, 0), to: "z1"), $dots.c$, name: "dots1", padding: 4pt)
  content((rel: (0.7, 0), to: "zi1"), $dots.c$, name: "dots2", padding: 4pt)
  content((rel: (0.9, 0), to: "zk"), $= x$)

  // Draw arrows and labels
  let arrow-style = (end: ">", fill: black, scale: 0.8, offset: 0.1)
  line("z0", "z1", mark: arrow-style, name: "z0-z1")
  content("z0-z1.mid", $f_1(z_0)$, name: "f1", anchor: "south", padding: (bottom: 3pt))

  line("dots1.east", "zi", mark: arrow-style, name: "z1-zi")
  content("z1-zi.30%", $f_i (z_1)$, name: "fi", anchor: "south", padding: (bottom: 3pt))

  line("zi", "zi1", mark: arrow-style, name: "zi-zi1")
  content("zi-zi1.mid", $f_(i+1) (z_i)$, name: "fi1", anchor: "south", padding: (bottom: 3pt))

  line("dots2.east", "zk", mark: arrow-style, name: "zi1-zk")
  content("zi1-zk.30%", $f_k (z_(k-1))$, name: "fk", anchor: "south", padding: (bottom: 3pt))

  // Draw distributions
  draw-distro(0, y-distro, p0, name: "d0")
  content("d0.south", $z_0 ~ p_0(z_0)$, anchor: "north", padding: (top: 3pt))

  draw-distro(2 * node-spacing, y-distro, pi, name: "di")
  content("di.south", $z_i ~ p_i(z_i)$, anchor: "north", padding: (top: 3pt))

  draw-distro(4 * node-spacing, y-distro, pk, name: "dk")
  content("dk.south", $z_k ~ p_k(z_k)$, anchor: "north", padding: (top: 3pt))
})