« home

Regular vs Bayes NN

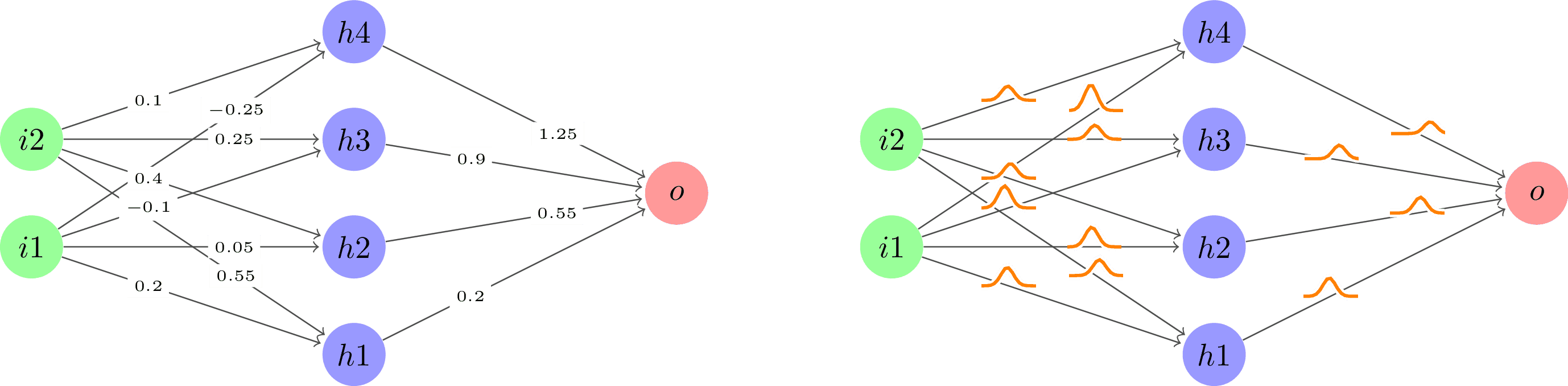
Comparison between regular neural networks and Bayesian neural networks. The diagram illustrates how Bayesian networks incorporate uncertainty in their predictions by treating weights as probability distributions rather than point values, leading to more robust predictions with uncertainty estimates.

Download

PNG PDF SVG

Code

regular-vs-bayes-nn.tex (62 lines)

\documentclass[tikz]{standalone}

\usetikzlibrary{calc}

\def\layersep{3cm}
\newcommand\nn[1]{
    % Input layer
    \foreach \y in {1,...,2}
        \node[neuron, fill=green!40] (i\y-#1) at (0,\y+1) {$i\y$};

    % Hidden layer
    \foreach \y in {1,...,4}
        \path node[neuron, fill=blue!40] (h\y-#1) at (\layersep,\y) {$h\y$};

    % Output node
    \node[neuron, fill=red!40] (o-#1) at (2*\layersep,2.5) {$o$};

    % Connect every node in the input layer with every node in the hidden layer.
    \foreach \source in {1,...,2}
        \foreach \dest in {1,...,4}
            \path (i\source-#1) edge (h\dest-#1);

    % Connect every node in the hidden layer with the output layer
    \foreach \source in {1,...,4}
        \path (h\source-#1) edge (o-#1);
}

\begin{document}
\begin{tikzpicture}[
    scale=1.2,
    shorten >=1pt,->,draw=black!70, node distance=\layersep,
    neuron/.style={circle,fill=black!25,minimum size=20,inner sep=0},
    edge/.style 2 args={pos={(mod(#1+#2,2)+1)*0.33}, font=\tiny},
    distro/.style 2 args={
        edge={#1}{#2}, node contents={}, minimum size=0.6cm, path picture={\draw[double=orange,white,thick,double distance=1pt,shorten >=0pt] plot[variable=\t,domain=-1:1,samples=51] ({\t},{0.2*exp(-100*(\t-0.05*(#1-1))^2 - 3*\t*#2))});}
      },
    weight/.style 2 args={
        edge={#1}{#2}, node contents={\pgfmathparse{0.35*#1-#2*0.15}\pgfmathprintnumber[fixed]{\pgfmathresult}}, fill=white, inner sep=2pt
      }
  ]
  \nn{regular}

  \begin{scope}[xshift=8cm]
    \nn{bayes}
  \end{scope}

  % Draw weights for all regular edges.
  \foreach \i in {1,...,2}
  \foreach \j in {1,...,4}
  \path (i\i-regular) -- (h\j-regular) node[weight={\i}{\j}];
  \foreach \i in {1,...,4}
  \path (h\i-regular) -- (o-regular) node[weight={\i}{1}];

  % Draw distros for all Bayesian edges.
  \foreach \i in {1,...,2}
  \foreach \j in {1,...,4}
  \path (i\i-bayes) -- (h\j-bayes) node[distro={\i}{\j}];
  \foreach \i in {1,...,4}
  \path (h\i-bayes) -- (o-bayes) node[distro={\i}{1}];
\end{tikzpicture}
\end{document}

regular-vs-bayes-nn.typ (196 lines)

#import "@preview/cetz:0.4.1": canvas, draw
#import "@preview/cetz-plot:0.1.2": plot
#import draw: bezier, circle, content, group, line, translate

#set page(width: auto, height: auto, margin: 8pt)

#canvas({
  let layer-sep = 3.5 // Horizontal separation between layers
  let node-sep = 1.5 // Vertical separation between nodes
  let arrow-style = (mark: (end: "stealth", scale: 0.7), stroke: gray + 0.7pt, fill: gray)

  // Helper function to draw a neuron
  let neuron(pos, fill: white, label: none, name: none) = {
    content(
      pos,
      if label != none { $#label$ },
      frame: "circle",
      fill: fill,
      stroke: none,
      radius: 0.4,
      padding: 3pt,
      name: name,
    )
  }

  // Helper function to calculate line angle and shift along it
  let line-shift(start, end, dist) = {
    let dx = end.at(0) - start.at(0)
    let dy = end.at(1) - start.at(1)
    let len = calc.sqrt(dx * dx + dy * dy)
    // Return shift vector components
    return (
      x: dist * dx / len,
      y: dist * dy / len,
    )
  }

  // Helper function to draw a weight label
  let weight-label(start, end, ii, jj, offset: 0) = {
    let mid-x = (start.at(0) + end.at(0)) / 2
    let mid-y = (start.at(1) + end.at(1)) / 2

    // Calculate shift along the line
    let shift = if offset != 0 {
      let s = line-shift(start, end, offset * 0.4)
      (s.x, s.y)
    } else { (0, 0) }

    content(
      (mid-x + shift.at(0), mid-y + shift.at(1)),
      [#calc.round(0.35 * ii - jj * 0.15, digits: 2)],
      frame: "rect",
      fill: white,
      stroke: none,
      padding: 1.5pt,
    )
  }

  // Helper function to draw a Gaussian distribution
  let gaussian(start, end, offset: 0, shift: 0) = {
    let width = 0.6
    let height = 0.25
    let x-mid = (start.at(0) + end.at(0)) / 2
    let y-mid = (start.at(1) + end.at(1)) / 2
    let mu = offset * 0.15

    // Calculate shift along the line
    let s = if shift != 0 {
      line-shift(start, end, shift * 0.4)
    } else { (x: 0, y: 0) }

    group({
      translate((x-mid - width / 2 + s.x, y-mid - height / 2 + s.y))
      plot.plot(size: (width, height), axis-style: none, {
        plot.add(style: (stroke: orange + 1pt, fill: orange.lighten(80%)), domain: (-1, 1), samples: 50, x => {
          let variance = 0.3 + calc.abs(offset) * 0.1
          let peak = 0.8 + calc.rem(calc.abs(offset), 0.4)
          peak * calc.exp(-5 * calc.pow(x - mu, 2) / variance)
        })
      })
    })
  }

  // Draw regular network
  group(name: "regular", {
    // Input layer
    for ii in range(2) {
      neuron(
        (0, (ii + 1) * node-sep + 1),
        fill: rgb("#90EE90"),
        label: "ii" + str(ii + 1),
        name: "ii" + str(ii + 1),
      )
    }

    // Hidden layer
    for ii in range(4) {
      neuron(
        (layer-sep, (ii + 1) * node-sep),
        fill: rgb("#ADD8E6"),
        label: "h" + str(ii + 1),
        name: "h" + str(ii + 1),
      )
    }

    // Output layer
    neuron(
      (2 * layer-sep, 2.5 * node-sep),
      fill: rgb("#FFB6C6"),
      label: "o",
      name: "o",
    )

    // Connect layers with weights
    for ii in range(2) {
      for jj in range(4) {
        let start = ("ii" + str(ii + 1))
        let end = ("h" + str(jj + 1))
        line(start, end, ..arrow-style)
        weight-label((0, (ii + 1) * node-sep + 1), (layer-sep, (jj + 1) * node-sep), ii + 1, jj + 1, offset: if ii
          == 0 { 1.5 } else { -1 })
      }
    }

    for ii in range(4) {
      let start = ("h" + str(ii + 1))
      line(start, "o", ..arrow-style)
      weight-label(
        (layer-sep, (ii + 1) * node-sep),
        (2 * layer-sep, 2.5 * node-sep),
        ii + 1,
        1,
      )
    }
  })

  // Draw Bayesian network
  group(name: "bayes", {
    // Shift everything right
    let x-offset = 3 * layer-sep

    // Input layer
    for ii in range(2) {
      neuron(
        (x-offset, (ii + 1) * node-sep + 1),
        fill: rgb("#90EE90"),
        label: "ii" + str(ii + 1),
        name: "ii" + str(ii + 1),
      )
    }

    // Hidden layer
    for ii in range(4) {
      neuron(
        (x-offset + layer-sep, (ii + 1) * node-sep),
        fill: rgb("#ADD8E6"),
        label: "h" + str(ii + 1),
        name: "h" + str(ii + 1),
      )
    }

    // Output layer
    neuron(
      (x-offset + 2 * layer-sep, 2.5 * node-sep),
      fill: rgb("#FFB6C6"),
      label: "o",
      name: "o",
    )

    // Connect layers with distributions
    for ii in range(2) {
      for jj in range(4) {
        let start = ("ii" + str(ii + 1))
        let end = ("h" + str(jj + 1))
        line(start, end, ..arrow-style)
        gaussian(
          (x-offset, (ii + 1) * node-sep + 1),
          (x-offset + layer-sep, (jj + 1) * node-sep),
          offset: ii - jj,
          shift: if ii == 0 { 1.5 } else { -1 },
        )
      }
    }

    for ii in range(4) {
      let start = ("h" + str(ii + 1))
      line(start, "o", ..arrow-style)
      gaussian(
        (x-offset + layer-sep, (ii + 1) * node-sep),
        (x-offset + 2 * layer-sep, 2.5 * node-sep),
        offset: ii,
      )
    }
  })
})