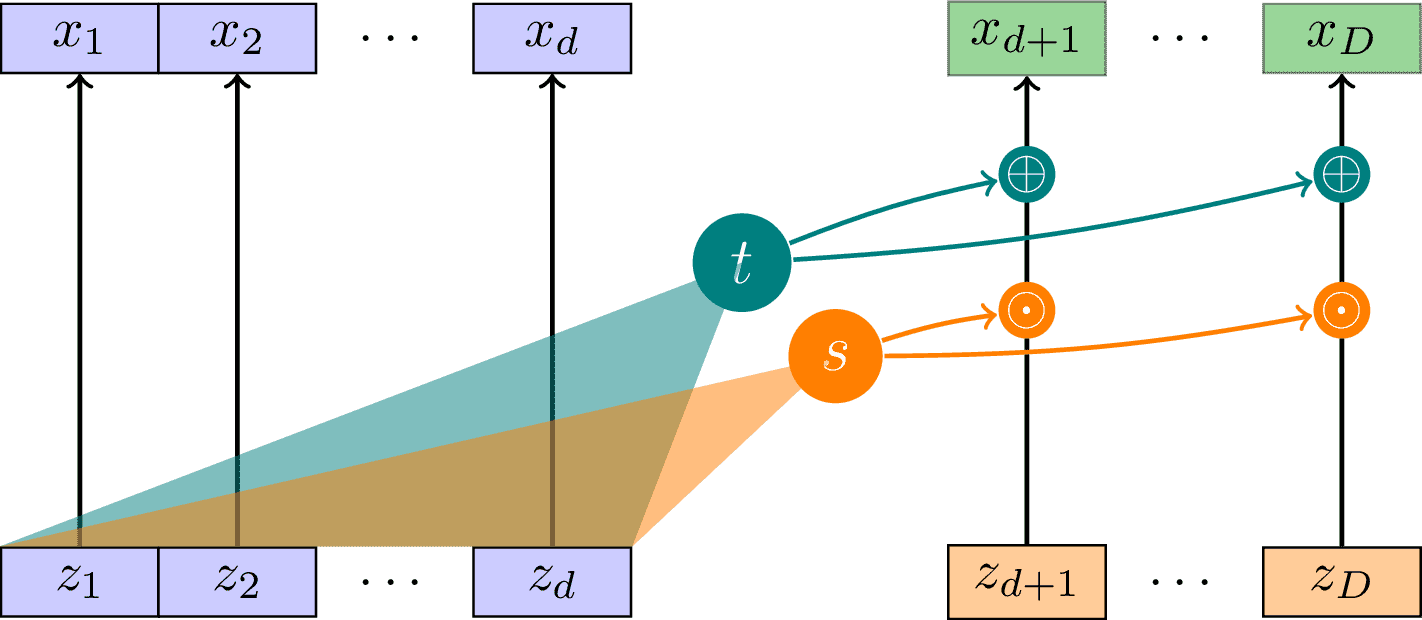
RNVP Affine Coupling Layer
Illustration of the real-valued non-volume preserving (RNVP) affine coupling layer as introduced in arxiv:1605.08803. Inspired by https://blog.evjang.com/2018/01/nf2.html.
Download
Code
LaTeX
rnvp-affine-coupling-layer.tex (57 lines)
\documentclass[tikz]{standalone}
\usetikzlibrary{calc,positioning}
\begin{document}
\begin{tikzpicture}[
thick, text centered,
box/.style={draw, thin, minimum width=1cm},
func/.style={circle, text=white},
]
% x nodes
\node[box, fill=blue!20] (x1) {$x_1$};
\node[box, fill=blue!20, right of=x1] (x2) {$x_2$};
\node[right of=x2] (xdots1) {\dots};
\node[box, fill=blue!20, right of=xdots1] (xd) {$x_d$};
\node[box, fill=green!60!black, text opacity=1, opacity=0.4, right=2 of xd] (xdp1) {$x_{d+1}$};
\node[right of=xdp1] (xdots2) {\dots};
\node[box, fill=green!60!black, text opacity=1, opacity=0.4, right of=xdots2] (xD) {$x_D$};
% z nodes
\node[box, fill=blue!20, below=3 of x1] (z1) {$z_1$};
\node[box, fill=blue!20, right of=z1] (z2) {$z_2$};
\node[right of=z2] (zdots1) {\dots};
\node[box, fill=blue!20, right of=zdots1] (zd) {$z_d$};
\node[box, fill=orange!40, right=2 of zd] (zdp1) {$z_{d+1}$};
\node[right of=zdp1] (zdots2) {\dots};
\node[box, fill=orange!40, right of=zdots2] (zD) {$z_D$};
% z to x lines
\draw[->] (z1) -- (x1);
\draw[->] (z2) -- (x2);
\draw[->] (zd) -- (xd);
\draw[->] (zdp1) -- (xdp1);
\draw[->] (zD) -- (xD);
% scale and translate functions
\node[func, font=\large, fill=teal, above left=0.1] (t) at ($(zd)!0.5!(xdp1)$) {$t$};
\fill[teal, opacity=0.5] (z1.north west) -- (t.center) -- (zd.north east) -- (z1.north west);
\node[func, font=\large, fill=orange, below right=0.1] (s) at ($(zd)!0.5!(xdp1)$) {$s$};
\fill[orange, opacity=0.5] (z1.north west) -- (s.center) -- (zd.north east) -- (z1.north west);
% feeding in s and t
\node[func, inner sep=0, fill=orange] (odot1) at ($(zdp1)!0.5!(xdp1)$) {$\odot$};
\node[func, inner sep=0, fill=teal] (oplus1) at ($(zdp1)!0.75!(xdp1)$) {$\oplus$};
\draw[orange, ->] (s) to[bend left=5] (odot1);
\draw[teal, ->] (t) to[bend left=5] (oplus1);
\node[func, inner sep=0, fill=orange] (odot2) at ($(zD)!0.5!(xD)$) {$\odot$};
\node[func, inner sep=0, fill=teal] (oplus2) at ($(zD)!0.75!(xD)$) {$\oplus$};
\draw[orange, ->] (s) to[bend right=5] (odot2);
\draw[teal, ->] (t) to[bend right=5] (oplus2);
\end{tikzpicture}
\end{document}
Typst
rnvp-affine-coupling-layer.typ (136 lines)
#import "@preview/cetz:0.3.2": canvas, draw
#set page(width: auto, height: auto, margin: 8pt)
#canvas({
import draw: line, content, rect, circle, hobby
// Define styles and constants
let node-width = 1
let node-height = 0.6
let horiz-sep = 1.2
let vert-sep = 4
let arrow-style = (end: "stealth", fill: black, scale: .5)
let (orange, blue, teal) = (rgb("#e8c268"), rgb("#63a7e390"), rgb("#008080"))
// Helper function for boxes
let box(pos, text, fill: none, name: none) = {
rect(
pos,
(rel: (node-width, node-height)),
fill: fill,
stroke: black + 0.3pt,
name: name,
)
content(name, text)
}
// Top row x nodes
box((0, 0), $x_1$, fill: blue, name: "x1")
box((horiz-sep, 0), $x_2$, fill: blue, name: "x2")
box((3 * horiz-sep, 0), $x_d$, fill: blue, name: "xd")
content(("x2", 50%, "xd"), text(size: 14pt)[$dots.c$], name: "xdots1")
// Green boxes with more spacing
box((5 * horiz-sep, 0), $x_(d+1)$, fill: orange, name: "xd-plus-1")
box((7 * horiz-sep, 0), $x_D$, fill: orange, name: "xD")
content(("xd-plus-1", 50%, "xD"), text(size: 14pt)[$dots.c$], name: "xdots2")
// Bottom row z nodes
box((0, -vert-sep), $z_1$, fill: blue, name: "z1")
box((horiz-sep, -vert-sep), $z_2$, fill: blue, name: "z2")
box((3 * horiz-sep, -vert-sep), $z_d$, fill: blue, name: "zd")
content(("z2", 50%, "zd"), text(size: 14pt)[$dots.c$], name: "zdots1")
// Orange boxes
box((5 * horiz-sep, -vert-sep), $z_(d+1)$, fill: orange, name: "zd-plus-1")
box((7 * horiz-sep, -vert-sep), $z_D$, fill: orange, name: "zD")
content(("zd-plus-1", 50%, "zD"), text(size: 14pt)[$dots.c$], name: "zdots2")
// Vertical connecting lines
line("z1", "x1", mark: arrow-style, name: "line1")
line("z2", "x2", mark: arrow-style, name: "line2")
line("zd", "xd", mark: arrow-style, name: "lined")
line("zd-plus-1", "xd-plus-1", mark: arrow-style, name: "line-d-plus-1")
line("zD", "xD", mark: arrow-style, name: "lineD")
// Scale and translate functions
let mid-x = 4 * horiz-sep
let mid-y = -vert-sep / 2
// Function triangles and circles
// Draw t triangle with lines
content(
(4.3 * horiz-sep, 0.4 * -vert-sep),
text(fill: white)[t],
frame: "circle",
name: "t-circle",
stroke: none,
fill: teal,
padding: 2pt,
)
line(
"z1.north-west",
"t-circle",
"zd.north-east",
fill: teal.transparentize(40%),
close: true,
stroke: none,
name: "t-triangle",
)
// Draw s triangle with lines
content(
(rel: (.6, -.75), to: "t-circle"),
text(fill: white, baseline: -1pt)[s],
frame: "circle",
name: "s-circle",
stroke: none,
fill: orange,
padding: 2pt,
)
line(
"z1.north-west",
"s-circle",
"zd.north-east",
fill: orange.transparentize(30%),
close: true,
stroke: none,
name: "s-triangle",
)
// Operation circles
for line-name in ("line-d-plus-1", "lineD") {
for (op, (color, label, pos)) in (
"odot": (orange, $dot.circle$, "40%"),
"oplus": (teal, $plus.circle$, "70%"),
).pairs() {
content(
line-name + "." + pos,
text(fill: white, baseline: -.2pt)[#label],
frame: "circle",
name: line-name + "-" + op,
stroke: none,
fill: color,
padding: .1pt,
)
}
}
// Connect s and t to operations
for line-name in ("line-d-plus-1", "lineD") {
hobby(
"s-circle",
line-name + "-odot",
mark: (..arrow-style, offset: 5pt),
stroke: orange + 0.75pt,
)
hobby(
"t-circle",
line-name + "-oplus",
mark: (..arrow-style, offset: 5pt),
stroke: teal + 0.75pt,
)
}
})