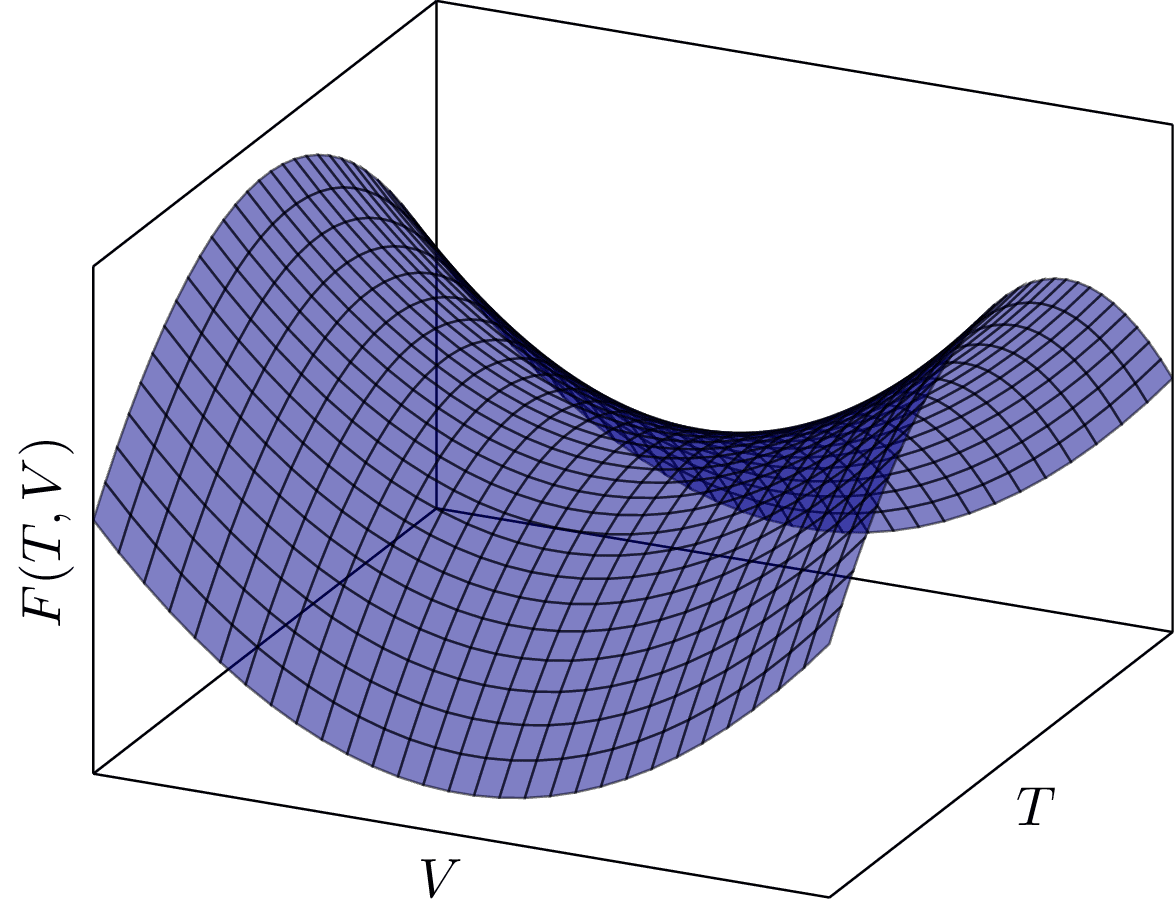
Saddle Point

mathconvexitycetztikz

This graph depicts a saddle point in three-dimensional space, which is a point in the domain of a function that is a local minimum in one direction and a local maximum in another. The depicted function $F(T, V)$ is quadratic in $T$ and $V$ , and the graph shows the convex and concave nature of the function along different axes.

Download

PNG PDF

Code

LaTeX

saddle-point.tex (16 lines)

\documentclass[svgnames]{standalone}

\usepackage{pgfplots}
\pgfplotsset{compat=newest}

\begin{document}

\begin{tikzpicture}
  \begin{axis}[samples=30,ticks=none,xlabel={$V$},ylabel={$T$},zlabel={$F(T,V)$}]

    \addplot3[surf,color=DarkBlue,opacity=0.5,domain=-2:2,faceted color=black] {x^2-y^2};
  \end{axis}
\end{tikzpicture}

\end{document}

Typst

saddle-point.typ (30 lines)

#import "@preview/plotsy-3d:0.1.0": plot-3d-surface

#set page(width: auto, height: auto)

#let saddle_func(x, y) = x * x - y * y

// Define a color function for the surface
#let color_func(x, y, z, x_lo, x_hi, y_lo, y_hi, z_lo, z_hi) = {
  return rgb("#00008B").transparentize(50%)
}

// Define domain and scaling
#let domain_size = 2
#let scale_factor = 0.2
#let (x_scale, y_scale, z_scale) = (0.5, 0.3, 0.15)
#let scale_dim = (x_scale * scale_factor, y_scale * scale_factor, z_scale * scale_factor)

// Plot the 3D surface
#plot-3d-surface(
  saddle_func,
  color-func: color_func,
  subdivisions: 8,
  xdomain: (-domain_size, domain_size),
  ydomain: (-domain_size, domain_size),
  // axis-labels: ($V$, $T$, $F(T,V)$), // Compiler error: Unexpected argument
  // axis-step: (1, 1, 2), // Adjust axis steps if needed
  // axis-label-size: 1.2em, // Adjust label size if needed
  // rotation-matrix: ((-2, 2, 4), (0, -1, 0)), // Optional: Adjust view angle
)