Torus Fundamental Domain

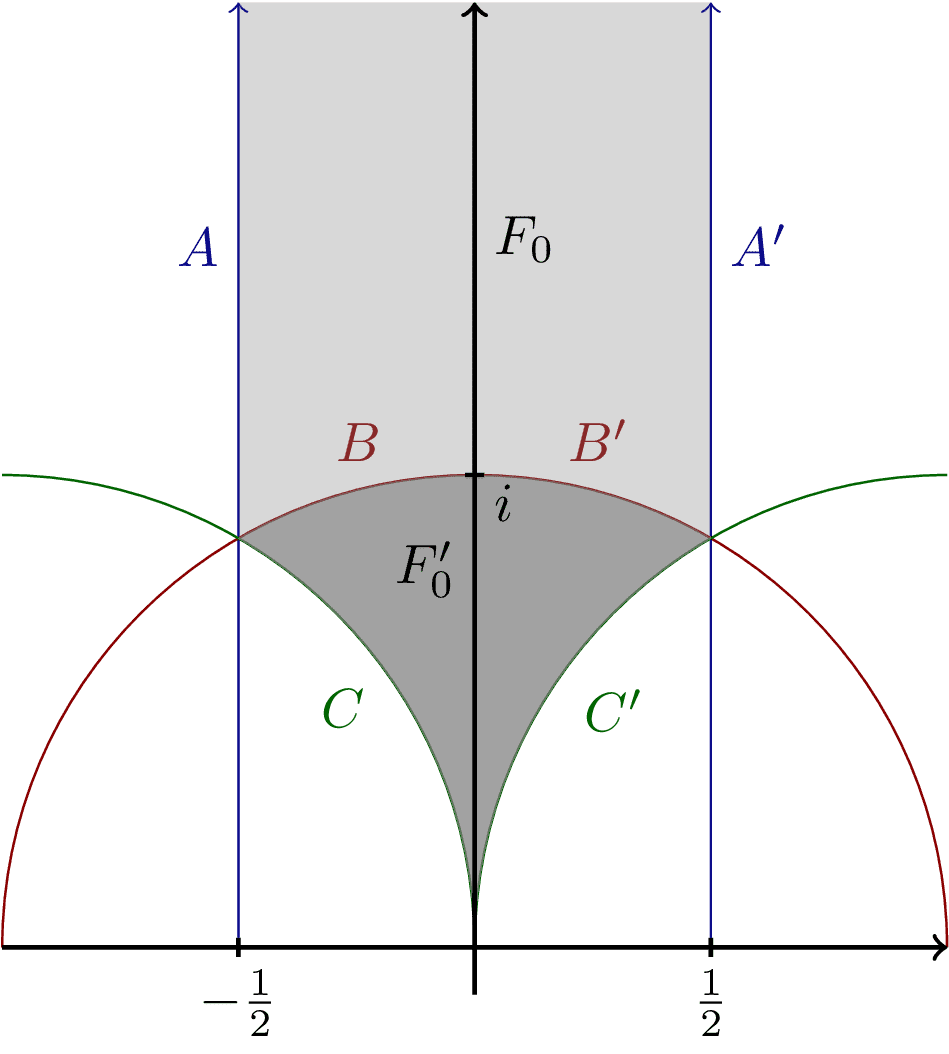
The light gray-shaded areas show a fundamental domain of a torus under modular transformations. The diagram shows the region in the complex plane that uniquely parametrizes inequivalent tori, bounded by the modular projective special linear group PSL(2,Z) transformations that identify physically equivalent fundamental domains for the action of $\Gamma$ on the upper half-plane.