2d Convolution
Creator: Petar Veličković (original)
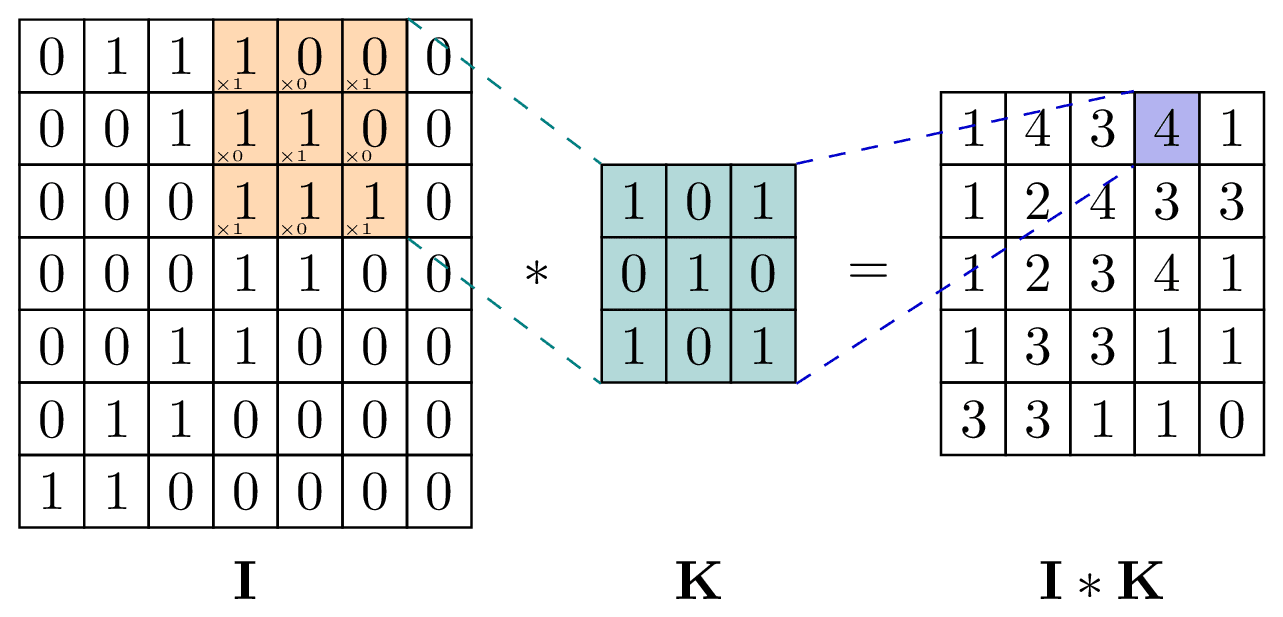
A two-dimensional convolution operator slides the kernel matrix across the target image and records elementwise products. Makes heavy use of the matrix environment in TikZ.
Download
Code
LaTeX
2d-convolution.tex (56 lines)
\documentclass[tikz]{standalone}
\usetikzlibrary{matrix, positioning}
\begin{document}
\begin{tikzpicture}[
2d-arr/.style={matrix of nodes, row sep=-\pgflinewidth, column sep=-\pgflinewidth, nodes={draw}}
]
\matrix (mtr) [2d-arr] {
0 & 1 & 1 & |[fill=orange!30]| 1 & |[fill=orange!30]| 0 & |[fill=orange!30]| 0 & 0\\
0 & 0 & 1 & |[fill=orange!30]| 1 & |[fill=orange!30]| 1 & |[fill=orange!30]| 0 & 0\\
0 & 0 & 0 & |[fill=orange!30]| 1 & |[fill=orange!30]| 1 & |[fill=orange!30]| 1 & 0\\
0 & 0 & 0 & 1 & 1 & 0 & 0\\
0 & 0 & 1 & 1 & 0 & 0 & 0\\
0 & 1 & 1 & 0 & 0 & 0 & 0\\
1 & 1 & 0 & 0 & 0 & 0 & 0\\
};
\node[below=of mtr-5-4] {$\mathbf I$};
\node[right=0.2em of mtr] (str) {$*$};
\matrix (K) [2d-arr, right=0.2em of str, nodes={draw, fill=teal!30}] {
1 & 0 & 1 \\
0 & 1 & 0 \\
1 & 0 & 1 \\
};
\node[below=of K-3-2] {$\mathbf K$};
\node[right=0.2em of K] (eq) {$=$};
\matrix (ret) [2d-arr, right=0.2em of eq] {
1 & 4 & 3 & |[fill=blue!80!black!30]| 4 & 1\\
1 & 2 & 4 & 3 & 3\\
1 & 2 & 3 & 4 & 1\\
1 & 3 & 3 & 1 & 1\\
3 & 3 & 1 & 1 & 0\\
};
\node[below=of ret-4-3] {$\mathbf{I * K}$};
\draw[dashed, teal] (mtr-1-6.north east) -- (K-1-1.north west);
\draw[dashed, teal] (mtr-3-6.south east) -- (K-3-1.south west);
\draw[dashed, blue!80!black] (K-1-3.north east) -- (ret-1-4.north west);
\draw[dashed, blue!80!black] (K-3-3.south east) -- (ret-1-4.south west);
\foreach \i in {1,2,3} {
\foreach \j in {4,5,6} {
\node[font=\tiny, scale=0.6, shift={(-1.2ex,-2ex)}] at (mtr-\i-\j) {$\times \pgfmathparse{int(mod(\i+\j,2))}\pgfmathresult$};
}
}
\end{tikzpicture}
\end{document}
Typst
2d-convolution.typ (140 lines)
#import "@preview/cetz:0.3.2": canvas, draw
#set page(width: auto, height: auto, margin: 5pt)
#canvas({
import draw: line, content, rect, on-layer
let cell-size = 0.6
let matrix-sep = 1.5
let highlight = rgb(255, 200, 150) // orange!30
let kernel-color = rgb("#9ae7e1") // teal!30
let result-color = rgb(200, 200, 255) // blue!30
// Helper to draw a matrix cell
let draw-cell(pos, value, fill: none, name: none) = {
rect(
pos,
(pos.at(0) + cell-size, pos.at(1) + cell-size),
fill: fill,
name: name,
stroke: .5pt,
)
if value != none {
content(
(pos.at(0) + cell-size / 2, pos.at(1) + cell-size / 2),
$#value$,
)
}
}
// Helper to draw a matrix
let draw-matrix(origin, shape, values, highlights: (), name: none) = {
let (rows, cols) = shape
for ii in range(rows) {
for jj in range(cols) {
let pos = (origin.at(0) + jj * cell-size, origin.at(1) - ii * cell-size)
let idx = ii * cols + jj
let cell-name = if name != none { name + "-" + str(ii) + "-" + str(jj) }
draw-cell(
pos,
if idx < values.len() { values.at(idx) },
fill: if (ii, jj) in highlights { highlight },
name: cell-name,
)
}
}
}
// Draw input matrix I
let input-origin = (0, 4)
let input-values = (
..(0, 1, 1, 1, 0, 0, 0),
..(0, 0, 1, 1, 1, 0, 0),
..(0, 0, 0, 1, 1, 1, 0),
..(0, 0, 0, 1, 1, 0, 0),
..(0, 0, 1, 1, 0, 0, 0),
..(0, 1, 1, 0, 0, 0, 0),
..(1, 1, 0, 0, 0, 0, 0),
)
draw-matrix(
input-origin,
(7, 7),
input-values,
highlights: ((0, 3), (0, 4), (0, 5), (1, 3), (1, 4), (1, 5), (2, 3), (2, 4), (2, 5)),
name: "I",
)
content(
(input-origin.at(0) + 7 * cell-size / 2, 0),
$bold(I)$,
name: "I-label",
)
// Draw multiplication symbol
content((rel: (1, 0), to: "I-3-6"), text(size: 18pt)[$*$], name: "times")
// Draw kernel matrix K
let kernel-origin = (input-origin.at(0) + 7 * cell-size + matrix-sep, input-origin.at(1) - 2 * cell-size)
let kernel-values = (1, 0, 1, 0, 1, 0, 1, 0, 1)
draw-matrix(
kernel-origin,
(3, 3),
kernel-values,
name: "K",
)
// Fill kernel matrix background
rect("K-0-0.north-west", "K-2-2.south-east", fill: kernel-color, stroke: none)
// Redraw matrix on top of background
draw-matrix(kernel-origin, (3, 3), kernel-values, name: "K")
content(
(kernel-origin.at(0) + 3 * cell-size / 2, 0),
$bold(K)$,
name: "K-label",
)
// Draw equals sign
content((rel: (1, 0), to: "K-1-2"), text(size: 18pt)[$=$], name: "equals")
// Draw result matrix
let result-origin = (kernel-origin.at(0) + 3 * cell-size + matrix-sep, input-origin.at(1) - cell-size)
let result-values = (
..(1, 4, 3, 4, 1),
..(1, 2, 4, 3, 3),
..(1, 2, 3, 4, 1),
..(1, 3, 3, 1, 1),
..(3, 3, 1, 1, 0),
)
draw-matrix(result-origin, (5, 5), result-values, name: "R")
// Draw highlighted cell in result matrix
on-layer(
-1,
rect("R-0-3.north-west", "R-0-3.south-east", fill: result-color, stroke: none),
)
content(
(result-origin.at(0) + 5 * cell-size / 2, 0),
$bold(I * K)$,
name: "R-label",
)
// Draw connection lines
let dash-style = (stroke: (dash: "dashed", paint: rgb(150, 220, 200)))
line("I-0-5.north-east", "K-0-0.north-west", ..dash-style)
line("I-2-5.south-east", "K-2-0.south-west", ..dash-style)
let result-style = (stroke: (dash: "dashed", paint: rgb(150, 150, 220)))
line("K-0-2.north-east", "R-0-3.north-west", ..result-style)
line("K-2-2.south-east", "R-0-3.south-west", ..result-style)
// Add small multiplication symbols in highlighted region
for ii in range(3) {
for jj in (3, 4, 5) {
content(
("I-" + str(ii) + "-" + str(jj) + ".south-west"),
text(size: 6pt)[×#calc.rem(ii + jj, 2)],
anchor: "south-west",
padding: 1pt,
)
}
}
})