Angular Momentum Quantization

physicsquantum mechanicsangular momentumspincetz

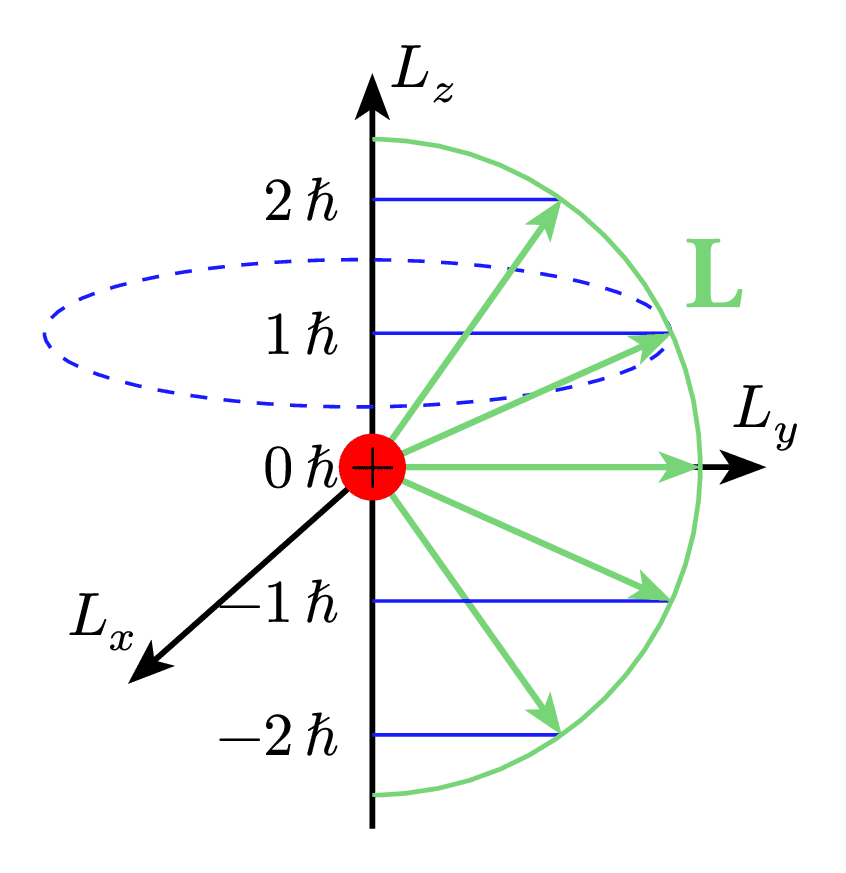
Visualization of the quantization of angular momentum (L) in quantum mechanics. The angular momentum magnitude |L| = √(l(l+1))ħ (green circle) is quantized, with the z-component (Lz) taking only discrete values mħ, where m ranges from -l to +l in integer steps. Each green arrow represents a possible orientation of the angular momentum vector, constrained by quantum mechanics to have specific z-components.