zT vs n

physicssolid state physicsthermodynamicscetztikz

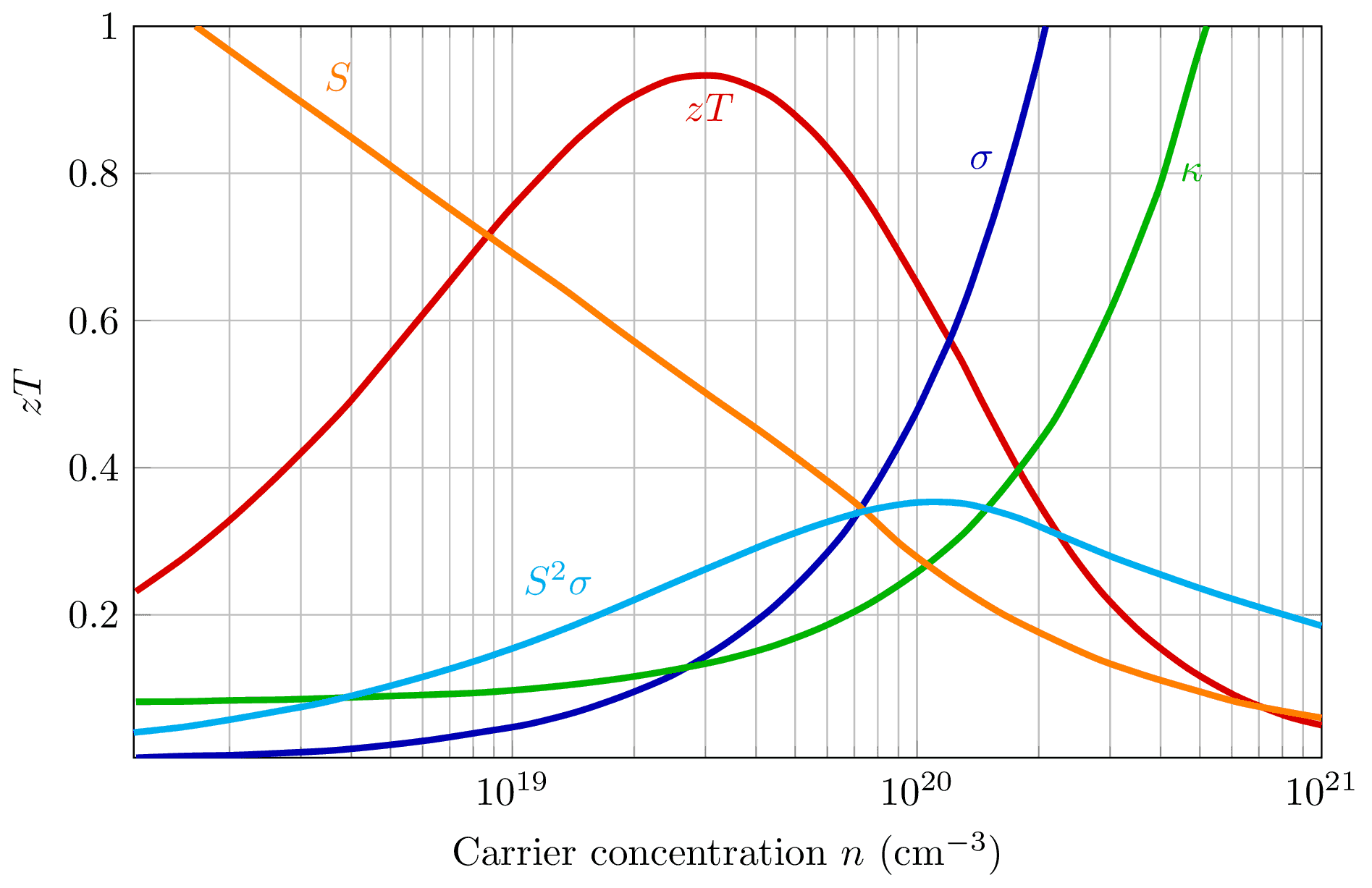
Thermoelectric figure of merit $zT$ vs carrier concentration $n$ for Bi2Te3 based on empirical data in $\alpha - \ln \sigma$ plot as a thermoelectric material performance indicator. Tuning $n$ for optimal $zT$ involves a compromise between thermal conductivity $\kappa$, Seebeck coefficient $S$ and electrical conductivity $\sigma$. Increasing the electrical conductivity $\sigma$ not only produces an increase in the electronic thermal conductivity $\kappa_\text{el}$ but also usually decreases the Seebeck coefficient $S$. This makes optimal $zT$ difficult to achieve. Plot scales are $\kappa [W / m K] \in [0,10]$, $S [mV] \in [0,500]$, $\sigma [1/(\Omega cm)] \in [0,5000]$.