Wyckoff Positions

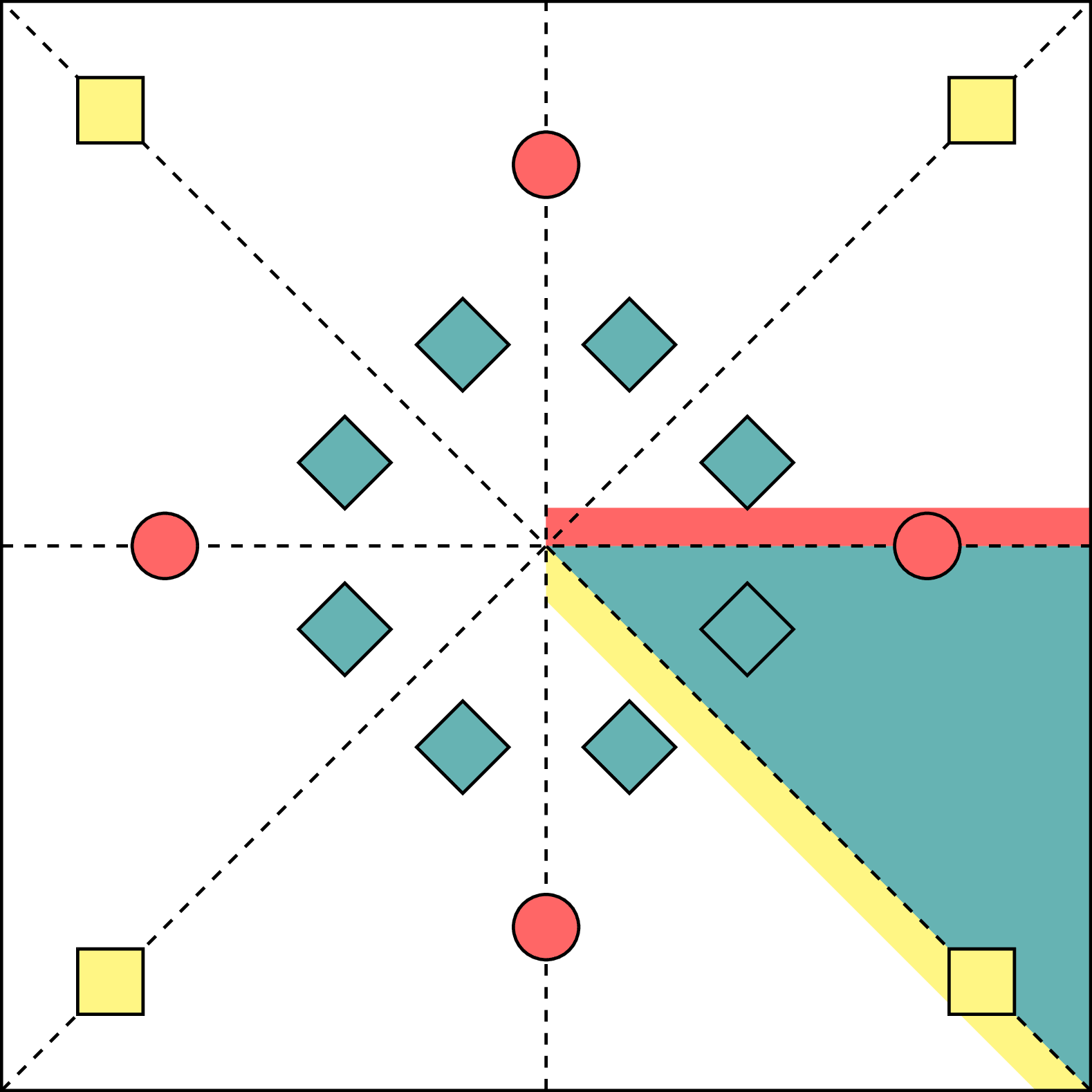
Unit cell representation of a 2D crystal with p4m symmetry and three occupied Wyckoff positions: 4-fold sites on the diagonal mirrors (yellow), 4-fold sites on the axial mirrors (red) and the 8-fold general position (teal). The shaded areas highlight the asymmetric unit and the site-symmetries of the atoms, indicating the region of the unit cell each atom is constrained to lie in by specifying its anonymized Wyckoff position. Reproduced from fig. 1 in "Wyckoff Set Regression for Materials Discovery" by Rhys Goodall, inspired by PyXtal docs.

Download

PNG PDF SVG

Code

wyckoff-positions.typ (98 lines)

#import "@preview/cetz:0.5.3": canvas, draw
#import draw: circle, content, group, line, rect, rotate

#set page(width: auto, height: auto, margin: 8pt, fill: none)

#canvas({
  let size = 5 // half the unit cell's side length
  let marker-size = 0.3 // half side of square markers, radius of circular ones
  let colors = (teal: rgb("#19d4d4"), yellow: rgb("#f3f380"), red: rgb("#f36969"))
  let square((x, y), fill) = rect(
    (x - marker-size, y - marker-size),
    (x + marker-size, y + marker-size),
    fill: fill,
  )

  // asymmetric unit (teal) and strips marking the mirror lines that constrain
  // the yellow (diagonal mirror) and red (axial mirror) Wyckoff positions
  line((0, 0), (size, 0), (size, -size), fill: colors.teal, close: true, stroke: none)
  let yellow-strip = ((size - .5, -size), (0, -.5), (0, 0), (size, -size))
  line(..yellow-strip, fill: colors.yellow, close: true, stroke: none)
  rect((0, 0), (size, 0.35), fill: colors.red, stroke: none)

  rect((-size, -size), (size, size))
  // mirror lines
  for (start, end) in (
    ((-size, -size), (size, size)),
    ((size, -size), (-size, size)),
    ((-size, 0), (size, 0)),
    ((0, -size), (0, size)),
  ) { line(start, end, stroke: (dash: "dashed")) }

  // 4 sites on the diagonal mirrors
  for x in (-0.8 * size, 0.8 * size) {
    for y in (-0.8 * size, 0.8 * size) { square((x, y), colors.yellow) }
  }
  // 4 sites on the axial mirrors
  for offset in (-0.7 * size, 0.7 * size) {
    circle((offset, 0), radius: marker-size, fill: colors.red)
    circle((0, offset), radius: marker-size, fill: colors.red)
  }
  // Legend naming the site types, the asymmetric unit and the mirror lines
  let legend-x = size + 1.2
  let legend-row(idx, swatch, label) = {
    let y = size - 0.6 - idx * 1.1
    group(swatch((legend-x, y)))
    content((legend-x + 0.8, y), text(size: 12pt, label), anchor: "west")
  }
  legend-row(0, pos => square(pos, colors.yellow), [4 sites on the diagonal mirrors])
  legend-row(
    1,
    pos => circle(pos, radius: marker-size, fill: colors.red),
    [4 sites on the axial mirrors],
  )
  legend-row(
    2,
    pos => group({
      rotate(45deg, origin: pos)
      square(pos, colors.teal)
    }),
    [8 sites in the general position],
  )
  legend-row(
    3,
    ((x, y)) => line(
      (x - 0.35, y + 0.3),
      (x + 0.35, y + 0.3),
      (x + 0.35, y - 0.4),
      fill: colors.teal,
      close: true,
      stroke: none,
    ),
    [asymmetric unit],
  )
  for (row, color, name, mirror) in (
    (4, colors.red, [red], [an axial]),
    (5, colors.yellow, [yellow], [a diagonal]),
  ) {
    legend-row(
      row,
      ((x, y)) => rect((x - 0.35, y - 0.15), (x + 0.35, y + 0.15), fill: color, stroke: none),
      [
        site symmetry: #name sites lie on #mirror mirror
      ],
    )
  }
  legend-row(
    6,
    ((x, y)) => line((x - 0.4, y), (x + 0.4, y), stroke: (dash: "dashed")),
    [mirror lines],
  )

  // 8 sites in the general position
  rotate(45deg)
  for idx in range(8) {
    let (angle, ring-radius) = (idx * 360deg / 8 + 22.5deg, 0.4 * size)
    square((ring-radius * calc.cos(angle), ring-radius * calc.sin(angle)), colors.teal)
  }
})