Ball Tree
Visualization of the Ball Tree algorithm, a space-partitioning data structure used for efficient nearest neighbor searches, particularly in high-dimensional spaces.
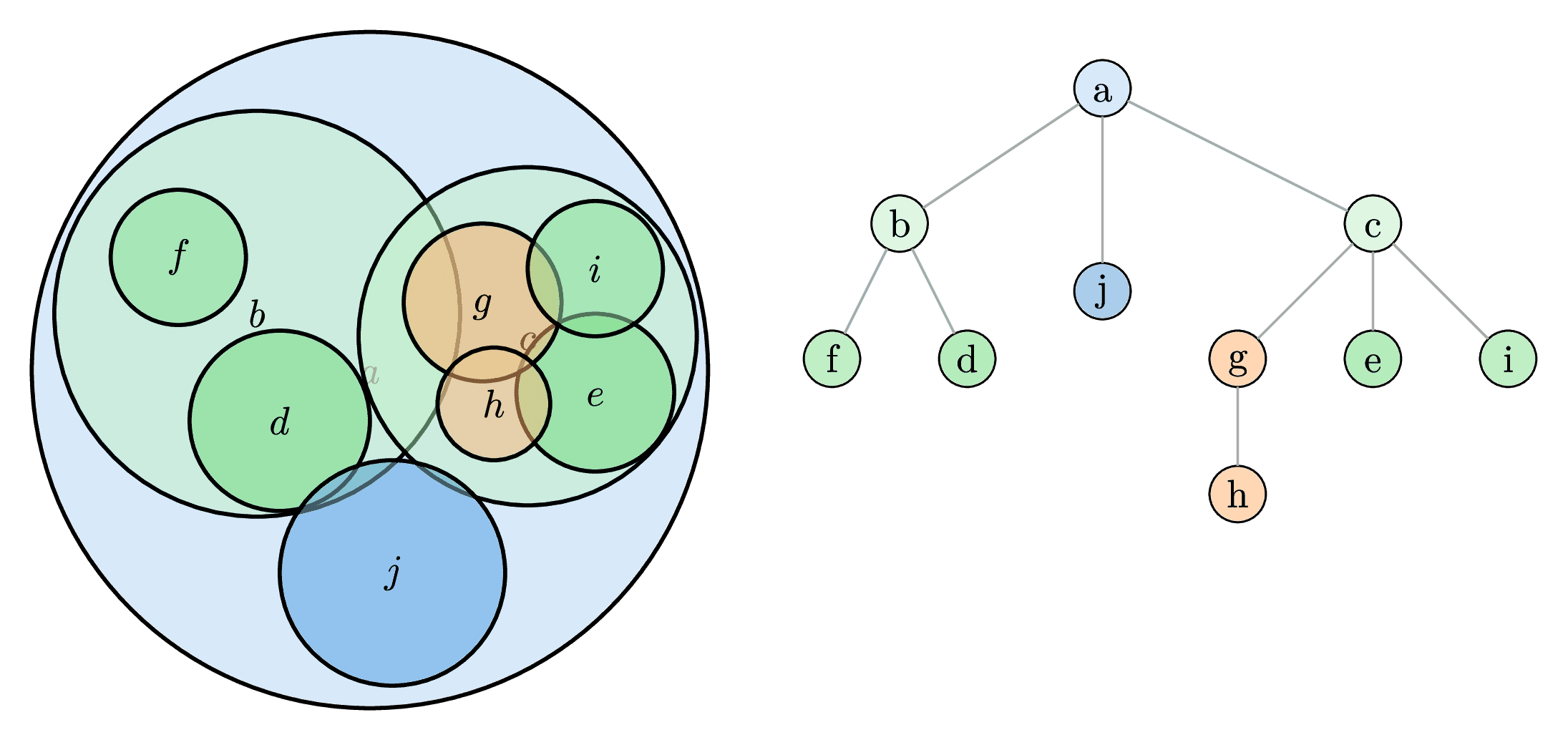
The left side illustrates the hierarchical partitioning of a dataset into nested hyperspheres (balls). Each ball represents a region of the space containing a subset of data points.
The right side shows the corresponding tree structure where each node represents a ball. Internal nodes represent larger balls encompassing the balls of their children, while leaf nodes contain the actual data points.
This hierarchical structure allows the search algorithm to prune large portions of the data space by comparing the query point's distance to the ball's center and radius, making it faster than exhaustive search, especially for high-dimensional non-uniformly distributed data.
Download
Code
Typst
ball-tree.typ (155 lines)
#import "@preview/cetz:0.3.4": canvas, draw
#import draw: line, content, circle
#set page(width: auto, height: auto, margin: 8pt)
#set text(size: 10pt) // Set default text size
#canvas({
// Styles
let node-radius = 0.25
let node-sep-x = 1.2 // Horizontal separation for tree
let node-sep-y = 1.2 // Vertical separation for tree
let tree-color = rgb("#6495ED") // Cornflower blue for tree nodes
let leaf-color = rgb("#FF6347") // Tomato red for leaf nodes
let arrow-style = (mark: (end: "stealth", fill: black, scale: 0.3), stroke: 0.6pt)
let tree-line-style = (stroke: (paint: gray, thickness: 0.6pt))
// Draw the circles with labels and different fills
circle(
(-3, 0),
radius: 3.0,
fill: blue.lighten(70%).transparentize(50%),
name: "circ-a",
)
content("circ-a", $a$)
circle(
(rel: (-1.0, 0.5), to: "circ-a"),
radius: 1.8,
fill: green.lighten(70%).transparentize(50%),
name: "circ-b",
)
content("circ-b", $b$)
circle(
(rel: (1.4, 0.3), to: "circ-a"),
radius: 1.5,
fill: green.lighten(70%).transparentize(50%),
name: "circ-c",
)
content("circ-c", $c$)
circle(
(rel: (0.2, -0.95), to: "circ-b"),
radius: 0.8,
fill: green.lighten(30%).transparentize(50%),
name: "circ-d",
)
content("circ-d", $d$)
circle(
(rel: (0.6, -0.5), to: "circ-c"),
radius: 0.7,
fill: green.lighten(30%).transparentize(50%),
name: "circ-e",
)
content("circ-e", $e$)
circle(
(rel: (-0.7, 0.5), to: "circ-b"),
radius: 0.6,
fill: green.lighten(40%).transparentize(50%),
name: "circ-f",
)
content("circ-f", $f$)
circle(
(rel: (-0.4, 0.3), to: "circ-c"),
radius: 0.7,
fill: orange.lighten(30%).transparentize(50%),
name: "circ-g",
)
content("circ-g", $g$)
circle(
(rel: (0.1, -0.9), to: "circ-g"),
radius: 0.5,
fill: orange.lighten(40%).transparentize(50%),
name: "circ-h",
)
content("circ-h", $h$)
circle(
(rel: (0.0, 1.1), to: "circ-e"),
radius: 0.6,
fill: green.lighten(40%).transparentize(50%),
name: "circ-i",
)
content("circ-i", $i$)
circle(
(rel: (0.2, -1.8), to: "circ-a"),
radius: 1.0,
fill: blue.lighten(30%).transparentize(50%),
name: "circ-j",
)
content("circ-j", $j$)
// --- Tree Structure (Right Side) ---
let tree_offset = (3.5, 2.5)
// Define colors for tree nodes matching partition circles
let node_colors = (
a: blue.lighten(70%).transparentize(50%),
b: green.lighten(70%).transparentize(50%),
c: green.lighten(70%).transparentize(50%),
d: green.lighten(30%).transparentize(50%),
e: green.lighten(30%).transparentize(50%),
f: green.lighten(40%).transparentize(50%),
g: orange.lighten(30%).transparentize(50%),
h: orange.lighten(40%).transparentize(50%),
i: green.lighten(40%).transparentize(50%),
j: blue.lighten(30%).transparentize(50%),
)
// Helper to draw tree nodes
let draw_tree_node(pos, label, name) = {
circle(pos, radius: node-radius, fill: node_colors.at(label), stroke: 0.5pt, name: name)
content(pos, $#label$)
}
// Level 0
draw_tree_node((tree_offset.at(0) + 0, tree_offset.at(1) + 0), "a", "node-a")
// Level 1
draw_tree_node((tree_offset.at(0) - 1.5 * node-sep-x, tree_offset.at(1) - node-sep-y), "b", "node-b")
draw_tree_node((tree_offset.at(0) + 2.0 * node-sep-x, tree_offset.at(1) - node-sep-y), "c", "node-c")
draw_tree_node((tree_offset.at(0) + 0, tree_offset.at(1) - node-sep-y * 1.5), "j", "node-j")
// Level 2
draw_tree_node((tree_offset.at(0) - 2.0 * node-sep-x, tree_offset.at(1) - 2 * node-sep-y), "f", "node-f")
draw_tree_node((tree_offset.at(0) - 1.0 * node-sep-x, tree_offset.at(1) - 2 * node-sep-y), "d", "node-d")
draw_tree_node((tree_offset.at(0) + 1.0 * node-sep-x, tree_offset.at(1) - 2 * node-sep-y), "g", "node-g")
draw_tree_node((tree_offset.at(0) + 2.0 * node-sep-x, tree_offset.at(1) - 2 * node-sep-y), "e", "node-e")
draw_tree_node((tree_offset.at(0) + 3.0 * node-sep-x, tree_offset.at(1) - 2 * node-sep-y), "i", "node-i")
// Level 3
draw_tree_node((tree_offset.at(0) + 1.0 * node-sep-x, tree_offset.at(1) - 3 * node-sep-y), "h", "node-h")
// Draw Tree Edges
line("node-a", "node-b", ..tree-line-style)
line("node-a", "node-c", ..tree-line-style)
line("node-a", "node-j", ..tree-line-style) // Connect a to j
line("node-b", "node-f", ..tree-line-style)
line("node-b", "node-d", ..tree-line-style)
line("node-c", "node-g", ..tree-line-style)
line("node-c", "node-e", ..tree-line-style) // Connect c to e
line("node-c", "node-i", ..tree-line-style)
line("node-g", "node-h", ..tree-line-style) // Connect g to h
// Line from e to h seems incorrect based on hierarchy, e contains i, g contains h
// line("node-e", "node-h", ..tree-line-style) // This edge seems incorrect based on left diagram, removing
})