Closed String Topologies

physicsstring theorytikz

When calculating scattering amplitudes via the path integral, we must sum over all possible world-sheet topologies. To characterize the types of world-sheets that have to be considered at each level of its perturbative expansion, string theory makes use of the following theorem:

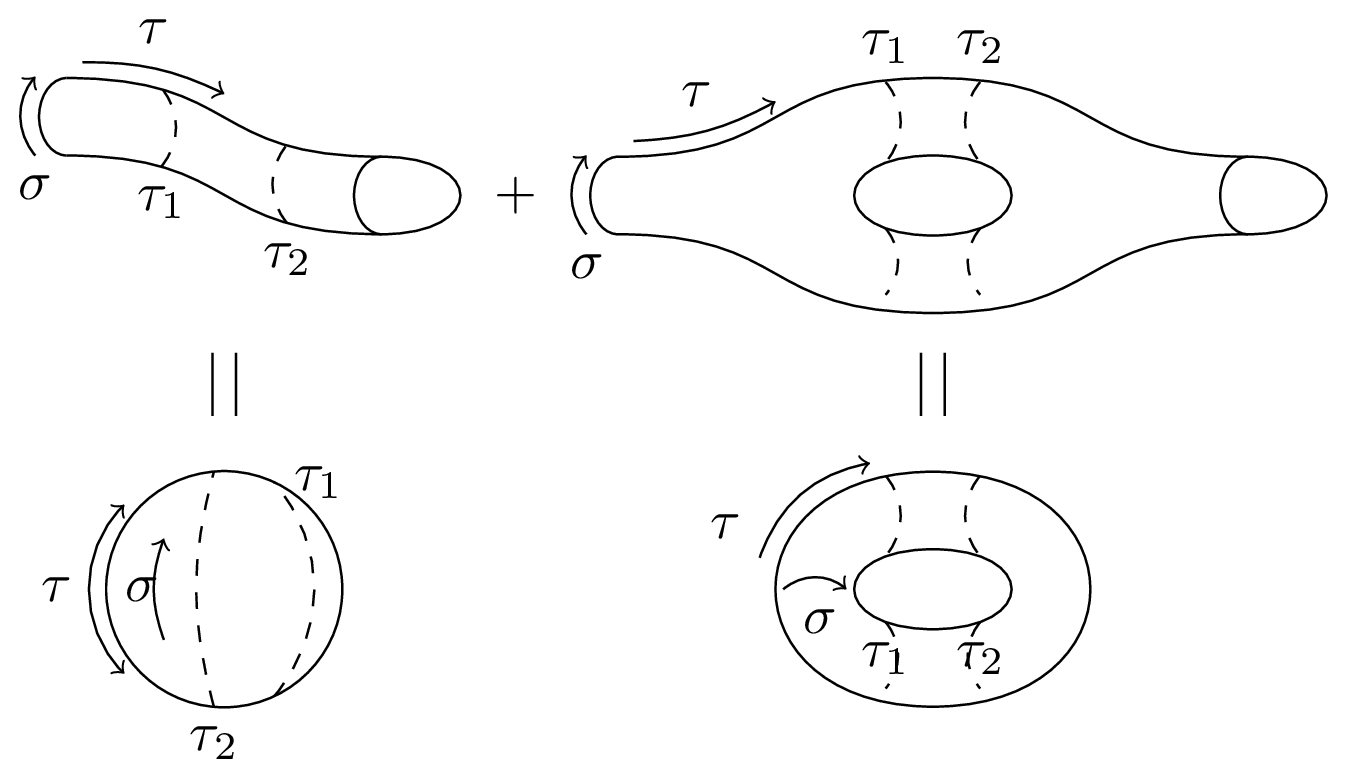
Every compact, connected, oriented two-dimensional manifold is topologically equivalent to a sphere with $g$ handles ($g$ for genus) and $b$ boundaries. A topological invariant of two-dimensional oriented surfaces is the Euler characteristic $\chi = 2 - 2g - b$.

What this boils down to is that we can obtain the topological characteristics of higher and higher loop-level world-sheet topologies by successively increasing in one-step increments the number of handles $g$ in case of the closed string and the number of boundaries $b$ for the open sector. This gives the topologies in this figure for the vacuum diagram of the closed sector up to one-loop level. For the open sector, see open string topologies.