home

Gas Pressure on Wall

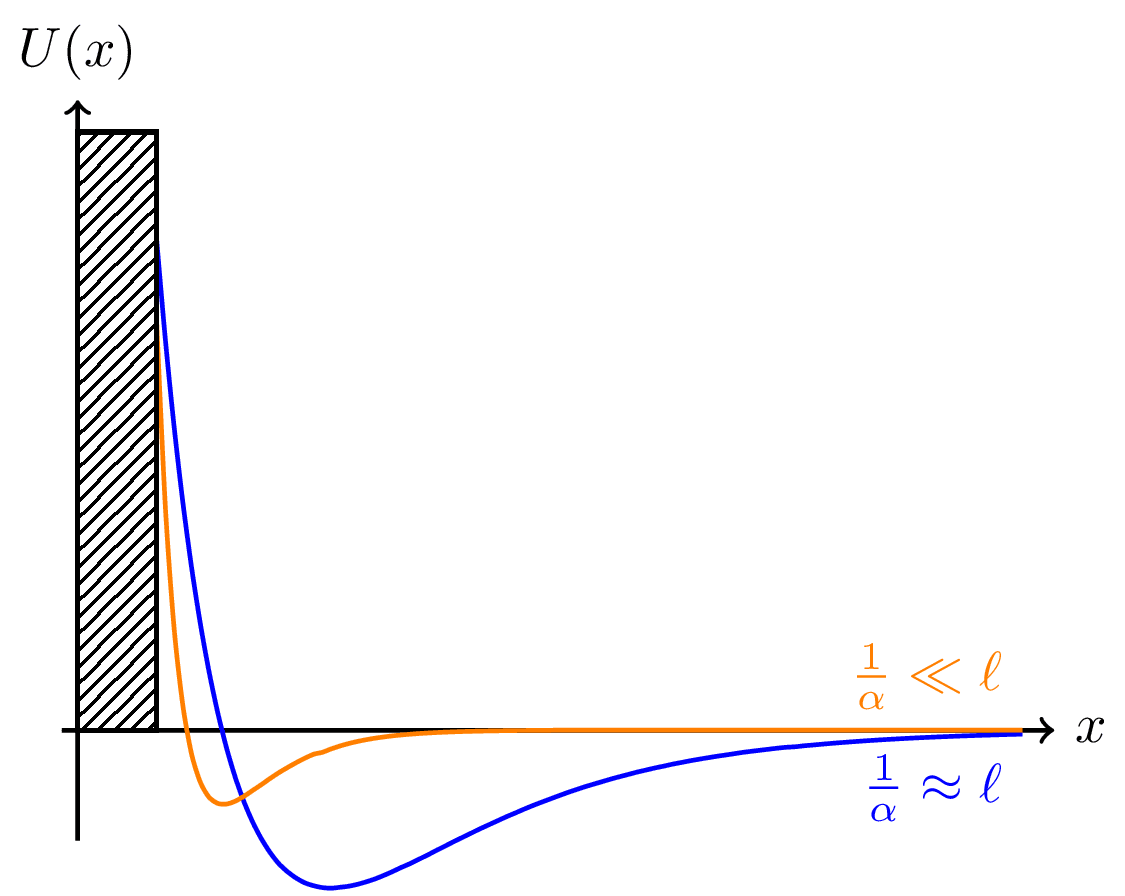
Exercise illustration: Compute the pressure of an ideal gas in three dimensions upon a wall at $x = 0$ that attracts molecules at large distance and repels them at smaller distance. Let the force be given by the potential $U(x) = -A \, e^{-\alpha x} + B \, e^{-2 \alpha x}$ , with $A,B > 0$ .

Download

PNG PDF SVG

Code

gas-pressure-on-wall.typ (78 lines)

#import "@preview/cetz:0.5.2": canvas, draw
#import draw: content, on-layer

#set page(width: auto, height: auto, margin: 8pt, fill: none)
#set text(size: 12pt)

#let hatched = tiling(size: (.2cm, .2cm))[
  #place(rect(width: 100%, height: 100%, fill: rgb("#cdd3da"), stroke: none))
  #place(line(start: (0%, 100%), end: (100%, 0%), stroke: 0.4pt))
]

#let lennard-jones(x, A, B, alpha) = {
  -A * calc.exp(-alpha * x) + B * calc.exp(-2 * alpha * x)
}

#canvas({
  let arrow-style = (mark: (end: ">", fill: black, scale: 0.7))
  let wall-width = 0.5

  draw.line((-0.1, 0), (6.2, 0), ..arrow-style, name: "x-axis")
  draw.line((0, -0.7), (0, 4), ..arrow-style, name: "y-axis")

  content((rel: (-0.2, 0.3), to: "x-axis.end"), $x$, name: "x-label")
  content((rel: (0.5, 0), to: "y-axis.end"), $U(x)$, name: "y-label")

  on-layer(
    1, // draw wall above pressure lines
    draw.rect(
      (0, 0),
      (wall-width, 3.6),
      fill: hatched,
      pattern: "north-east-lines",
      stroke: 0.75pt,
    ),
  )

  let samples = 100
  let dx = (6 - wall-width) / samples

  // First curve (blue)
  let (A1, B1, alpha1) = (10, 25, 1)

  for ii in range(samples - 1) {
    let x1 = wall-width + ii * dx
    let x2 = x1 + dx
    let y1 = lennard-jones(x1, A1, B1, alpha1)
    let y2 = lennard-jones(x2, A1, B1, alpha1)
    draw.line(
      (x1, y1),
      (x2, y2),
      stroke: blue,
      name: if ii == 67 { "blue-curve-label-pos" } else { none },
    )
  }
  content((rel: (0, -.45), to: "blue-curve-label-pos.mid"), text(
    fill: blue,
  )[$1 \/ alpha << ell$])

  // Second curve (orange)
  let (A2, B2, alpha2) = (15, 120, 3)

  for ii in range(samples - 1) {
    let x1 = wall-width + ii * dx
    let x2 = x1 + dx
    let y1 = lennard-jones(x1, A2, B2, alpha2)
    let y2 = lennard-jones(x2, A2, B2, alpha2)
    draw.line(
      (x1, y1),
      (x2, y2),
      stroke: orange,
      name: if ii == 67 { "orange-curve-label-pos" } else { none },
    )
  }
  content((rel: (0, .4), to: "orange-curve-label-pos.mid"), text(
    fill: orange,
  )[$1 \/ alpha << ell$])
})