Grand Canonical Occupation Fluctuations

physicsstatistical mechanicscetztikz

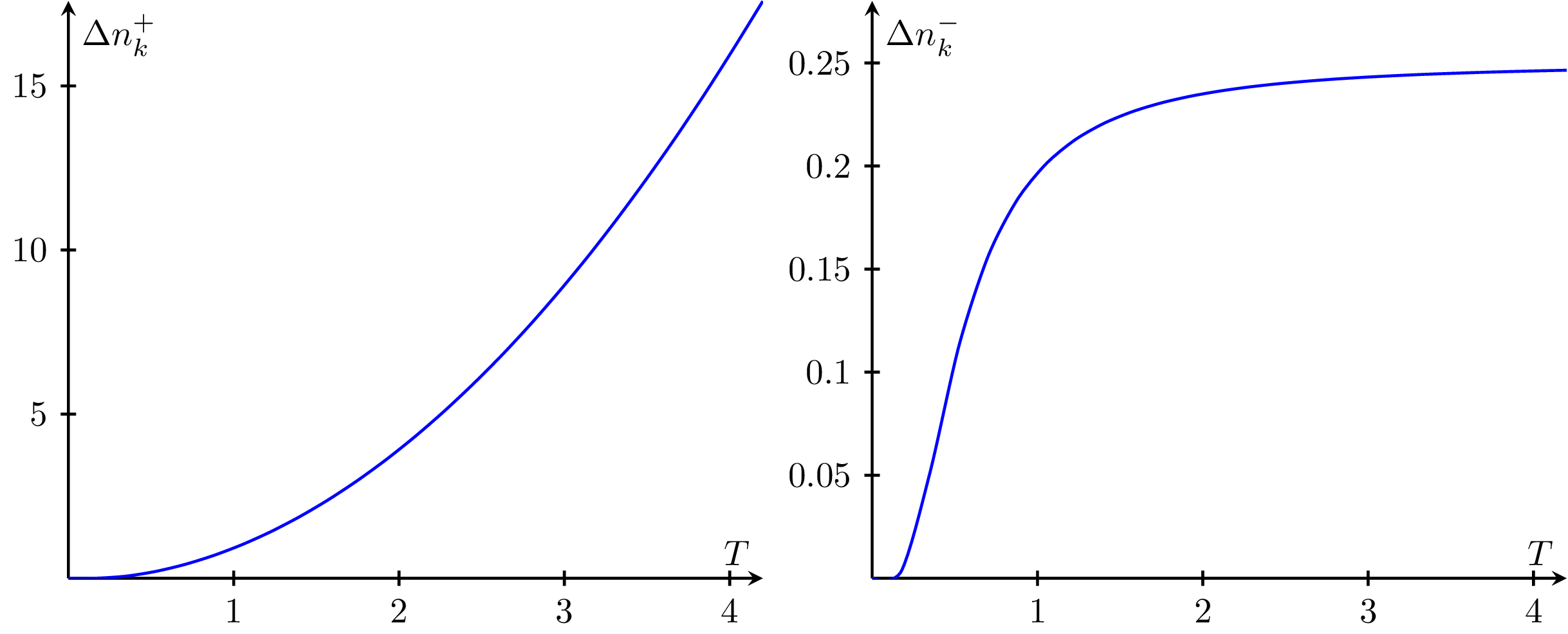
Number fluctuations of the occupation probability〈nk〉of a single mode k in an ideal Bose and Fermi gas in the grand canonical ensemble. Used in Exercise Sheet 11 of Statistical Physics by Manfred Salmhofer (2016), available at https://janosh.dev/physics/statistical-physics.